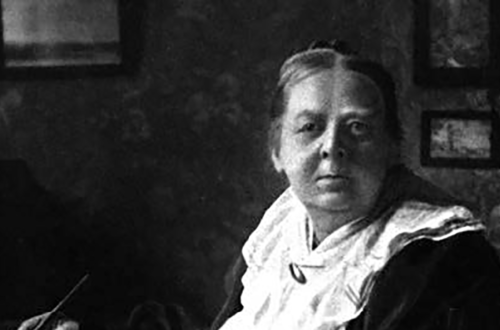Delta-K Volume 26 Issue 2

Journal of the Mathematics Council of the Alberta Teachers’ Association

Volume 26 Issue 2, June 1987

Direction

The junior and senior high school mathematics curricula are being reviewed, and it is assumed that the changes being considered will reflect the recommendations of the Review of Secondary Education report. Of particular importance to mathematics teachers is the statement that students should become critical thinkers. Problem-solving skills and strategies are a component of thinking.

Subsequent to the development of the article “Problem-Solving Relationships in Algebra,” I had the opportunity to present the content of the article at two workshops. Preliminary remarks included my view that in the future: (1) problems chosen should introduce the student to thinking procedures and the logical deductive nature of mathematics; (2) other problems should reflect or show an application of mathematics theory in a nontext problem situation; (3) another category of problems should show the need for intuitive or other thinking skills; and (4) problems should be selected from other disciplines to show that the mathematical problem-solving strategies also apply in other subjects.

During one of the workshops, a teacher asked: “John, do you have any research evidence that the use of different symbols will transfer into the algebraic approach?” The logical-deductive mode of thinking was evident. The question received an honest answer: “No!” I had not, and have not since then, read an article on the potential of this problem in introducing algebraic concepts. An equally academic response could have been: “Do you have any research evidence to show that transfer of thought processes from an intuitive to a deductive approach does not happen?” An issue is defined. Is mathematics purely logical deductive, or can mathematics be done in other thinking modes? As students become more proficient at organizing thought, they should become more proficient in the logical-deductive mode.

At the University of Lethbridge, I encounter many highly successful education students with grade point averages greater than three (on a four-point scale) who detest mathematics, who view mathematics as a system of rules, and who do not enjoy mathematics. The irony of the situation is that these education students have been taught mathematics in a logical-deductive manner, and those who teach mathematics will probably emulate the teachers who taught them mathematics.

Will the new Alberta secondary mathematics curriculum provide resource materials that encourage a problem-solving approach? Will the problems be coordinated to reflect content? Will the classroom environment be organized to encourage students to think? Both issues are the prerogative of the mathematics teacher.

Comments

The MCATA executive authorized this larger issue of delta-K so that some of the presentations delivered at the NC’IM Canadian Conference held in Edmonton, October 16-18, 1986, could be shared with a larger audience.

John Heuver’ s letter (below) is the first that the editor has received. Art Jorgensen provides a tribute to Joan Worth, the second recipient of the Mathematics Educator of the Year Award. Gary Hill of fers opinions on teaching problem solving. James Sherrill ana lyzes some problems and shows how they can be solved without using mathematical-deductive, algebraic reasoning. Student thinking, often the result of instruction, is analyzed by Eric Wood. Bonnie Litwiller and David Duncan present a problem-solving situation using an addition table, and explore patterns. Is there an al gebraic base for the patterns? Irvin Burbank uses inductive thinking to solve probability problems.

Two articles on evaluation of problem solving are presented by Marie Hauk and Gary Flewelling. Flewelling’s article allows teachers to rate themselves on the degree to which they make problem solving a part of their classroom environment.

Marshall Bye and Bob Midyette encourage the use of problems that support the core curriculum. John Percevault and Mary-Jo Maas demonstrate how problems used at the elementary school level can al so be ap plied at the junior and senior high school levels. Two problems are presented by Kevin Sherratt and Karen Gibling.

John B. Percevault

Front Matter

2 – 3

EDITORIAL

John B. Percevault

4 – 5

A Tribute to Joan Worth

Arthur- Jorgensen

6 – 9

Let’s Do Some Problem Solving in Junior High

Gary Hill

10 – 18