Delta-K
Journal of the Mathematics Council of the Alberta Teachers’ Association
Volume 55 Issue 2, March 2019
12 to 14
Integrating Math and Music (for Grades 7-12)
Catherine Schmidt-Jones
The material for this article is reprinted with permission from https://cnx.org/contents/qx- CNZS4M@9/Music-and-Math. Textbook content produced by Catherine Schmidt-Jones is licensed under a Creative Commons Attribution License 3.0 licence. Download for free at http://cnx.org/contents/a6108d65-2e0c-4fa8-9a2f-83072111cf71@9. Minor amendments have been made in accordance with ATA style.
Junior High Problem
Reading Time Signatures
You may have noticed that the time signature looks a little like a fraction in arithmetic. Filling up measures feels a little like finding equivalent fractions, too. In 4/4 time, for example, there are four beats in a measure and a quarter note gets one beat, so four quarter notes would fill up one measure. But so would any other combination of notes and rests that equals four quarters: one whole, two halves, one half plus two quarters, a half note and a half rest, and so on. If the time signature is 3/8, any combination of notes that adds up to three eighths will fill a measure. Remember that a dot is worth an extra half of the note it follows.

Tasks
1. Write four measures of music in each time signature:
a. 2/4 time
b. 3/8 time
c. 6/4 time
2. Share with a partner to clap each. (From https://cnx.org/contents/aBABIQ76@16/ Time-Signature)
High School Problem
The pitch of a note is how high or low it sounds. Musicians often find it useful to talk about how much higher or lower one note is than another. This distance between two pitches is called the interval between them. In Western music, the smallest interval from one note to the next closest note higher or lower is called a half step or semitone.
Major Scales
To find the rest of the notes in a major key, start at the tonic and go up following this pattern: whole step, whole step, half step, whole step, whole step, whole step, half step. This will take you to the tonic one octave higher than where you began, and includes all the notes in the key in that octave.
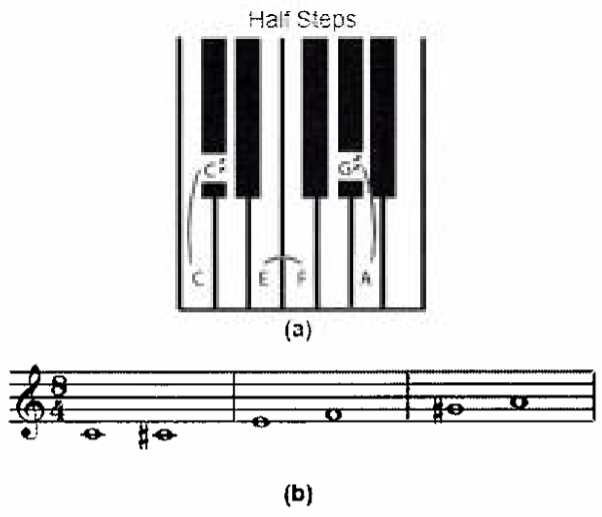
These major scales all follow the same pattern of whole steps and half steps. They have different sets of notes because the pattern starts on different notes.

Task
- Calculate the equal temperament frequency ratio of the tonic/first note to the following to the nearest ten thousandth.
- Calculate the difference between the equal temperament frequency ratio and the harmonic series frequency ratio.
- Finally, calculate the fractional equivalent to the harmonic series frequency ratio. (Please leave the frequency ratios and approximate difference columns blank for student input, and leave the last column blank for student input labelled “fraction value.”)
- Now investigate the sound of each compared to the tonic note. What do you notice about the pattern of differences and the sounds? What is the general relationship about the difference column to the sounds they make compared to the tonic note?
Comparing the Frequency Ratios for Equal Temperament and Pure Harmonic Series






