Timothy Sibbald
Through considering the problem of finding four points on the sides of a triangle that form a square, teachers can explore a variety of teaching possibilities. This article begins with an approach for intermediate math students and develops further methods suited to senior math students.
I conjecture that every triangle has four points on its sides that form a square. Whether this conjecture is true or not, the instructional value lies in having students determine where the square is for various triangles and whether the conjecture is true. The approach taken here is tiered in order to allow teachers to assess the suitability of the task for different grade levels.
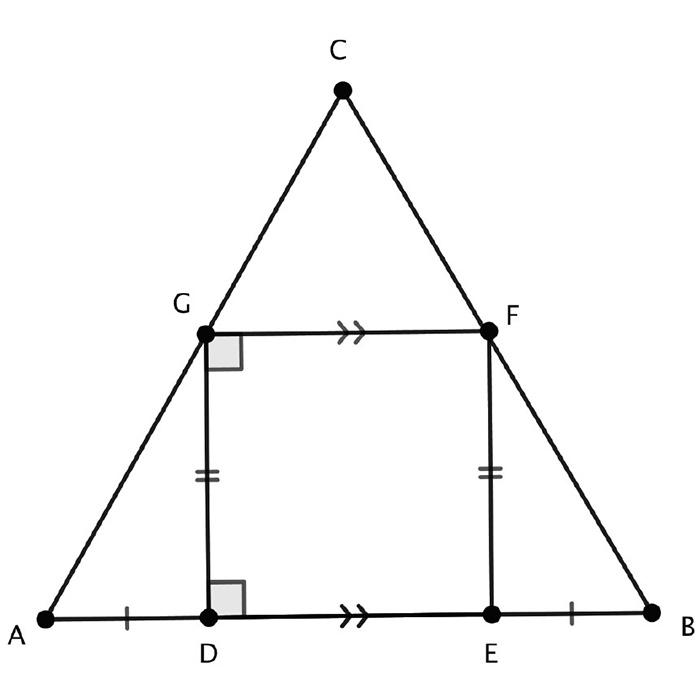
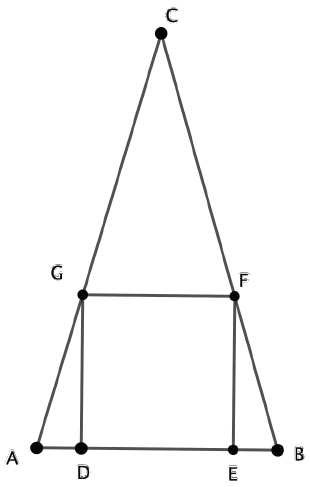
Teachers can make this question accessible to intermediate students by looking at special triangles. To begin, consider an equilateral triangle. The geometry is shown in Figure 1 and has been augmented with various properties explained below. For students, constructing diagrams using dynamic geometry software provides a starting point for thinking about the location of the square.
For this diagram, the equilateral triangle, ABC, was constructed in GeoGebra as a regular polygon, and then two points, D and E, were placed in arbitrary positions on side AB. Line segments perpendicular to AB were extended up from D and E to G and F, respectively, and a line segment, GF, was added to make the quadrilateral DEFG. The points D and E were moved along AB until the quadrilateral DEFG appeared, by visual inspection, to be a square. This process is not exact, but it is sufficient to provide a circumstance suitable for talking about properties in intermediate grades. The conjecture that an equilateral triangle can have an inscribed square now seems quite plausible, albeit unproven.
Suppose DEFG is a square in the equilateral triangle ABC and that they share an axis of symmetry. This means that AD has an equal length to BE. Since DEFG is a square, DE = GF = DG = EF. Since DEFG is a square, DE is parallel to GF. The geometry is quite good for students to prepare a formal explanation that ADG is congruent to BEF. In addition, although it is more challenging, students can determine that CFG is an equilateral triangle (hint: add the line of symmetry to make two congruent triangles).
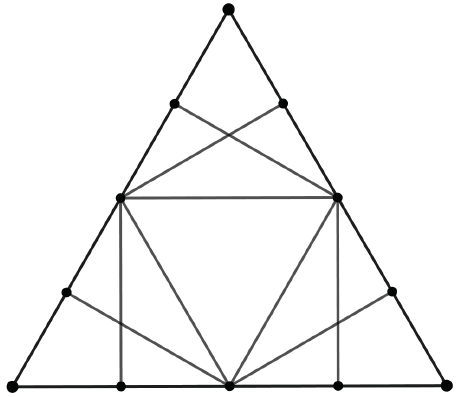
Last, notice that ABC has rotational symmetry, and any of the three sides could be selected as the side with two vertices. This implies that there are three possible squares, and adding the other two squares generates Figure 2. This facilitates a variety of classroom questions: Can you find a rhombus? How many kite shapes can you find? What is the relationship between the areas of a hexagon, three kites and an equilateral triangle? And, of course, there is the classic question of how many triangles appear in Figure 2.
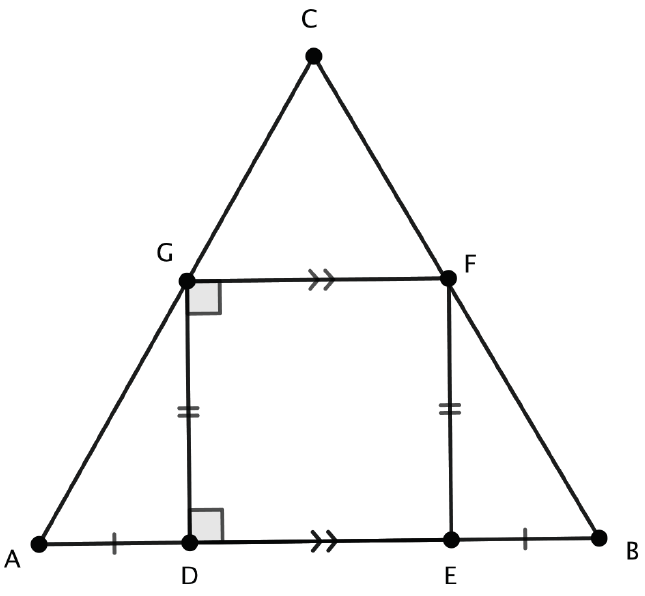
An isosceles triangle has an inscribed square when there are two vertices on the side with the unique length (Figure 3). This case is similar to the equilateral case because the square shares its axes of symmetry with the triangle. The isosceles case allows for differentiation of instruction where students can explore whether there are any squares with only one vertex on the side of unique length. This scenario is shown in Figure 4.
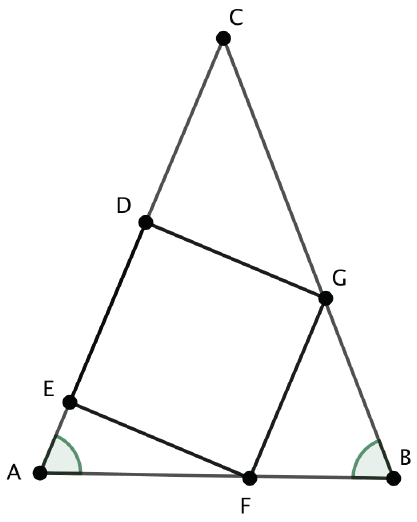
In Figure 4, ∠ A and ∠ B are equal, and ∠ AEF is a right angle, so ∠ AFE is the complement of ∠ A. However, ∠ AFE is also the complement of ∠ BFG (since ∠ EFG is a right angle). That means that ∠ BFG is equal to ∠ B, and therefore FBG is an isosceles triangle. This can be a teachable moment in which similar triangles are introduced.
The discovery that FBG is isosceles leads to looking for other characteristics and making conjectures. Students may suggest that CDG is isosceles, but it isn’t generally—only when ∠ C is 45°. Exploring such ideas is an important activity in the development of geometrical thinking in the intermediate grades.
High school, particularly analytic geometry, is well suited to addressing this problem more generally. Suppose two vertices of the triangle are A(0, 0) and B(1, 0). Let the third vertex be C(p, q). There is a need to discuss the domain for this point. All triangles can be formed with 0 ≤ p < 1. In particular, when q is small, ∠ C will be obtuse.
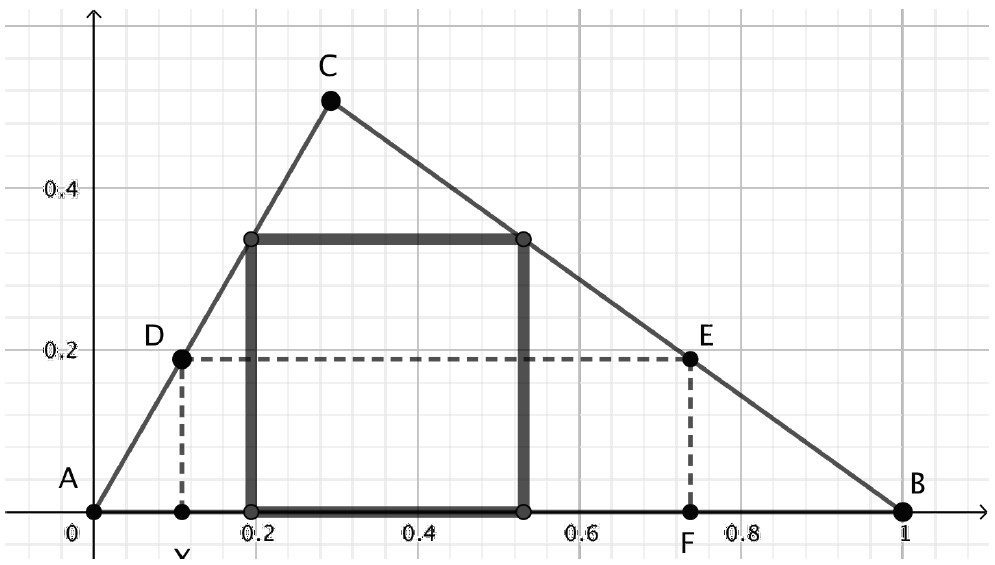
This set-up also permits one to choose side AB as the side with two vertices of the square—without loss of generality. Considering these choices as an approach to simplify the interpretation is an important instructional moment in analytic geometry teaching. The set-up is shown in Figure 5, with a rectangle that is explained below.
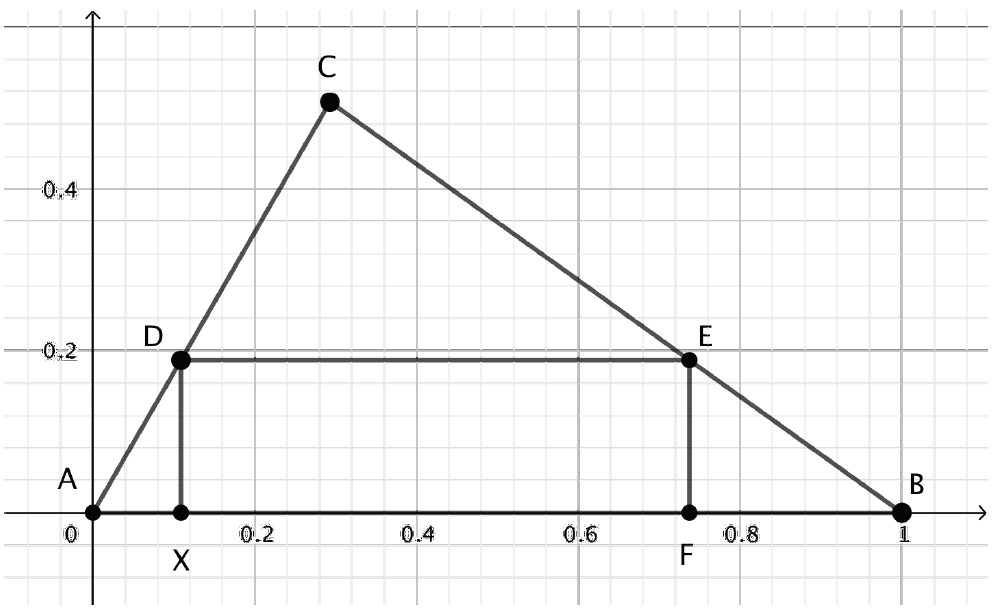
In Figure 5, the approach to finding the square is to add a point X at (x, 0) that generates a rectangle. First, XD is perpendicular to the x-axis; then, DE is perpendicular to XD; and, finally, EF is perpendicular to DE. The intersection points can be found, and a rectangle must arise. This explanation is well suited to instruction because it simply says that a rectangle can be made without providing the instructional details. Having students write down a recipe of calculation steps, with no actual calculations, helps organize their thinking and serves to put the organizational steps into place before focusing on the details. For example,
A method for finding the square is to determine the equation of line AC so that both components of coordinate D can be written algebraically in terms of x. Then, by determining the equation of line BC, we can write the components of point E algebraically in terms of x. The distance XF can then be determined algebraically, as well as the distance XD. Setting these two distances equal to each other will provide an equation that is solved for x. That value of x will define the square inside the triangle (for the general values of p and q).
The specific steps are as follows:
Step 1. Find the equation of line AC.
This is direct variation with a y-intercept of 0. The equation is y = (q/p)x.
Step 2. Write out both coordinates of point D.
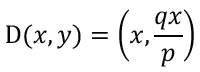
Step 3. Find the equation of line BC.
This can be done in various ways. I will use slope-point form. Also, x is already in use, so I need to use a different letter. In the equation, I use t, which will ultimately depend on x:
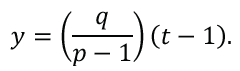
Step 4. Write out both coordinates of point E.
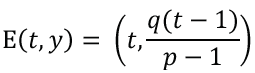
Step 5. Determine distance XF.
Since x is the left x-coordinate of the rectangle and t is the right x-coordinate, the distance is t − x.
Step 6. Determine distance XD.
This is the y-coordinate of point D, which is qx/p.
Step 7. Set distance XF equal to XD, and solve for t (in terms of p and q).
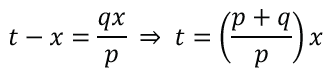
This is major progress, but the use of two variables, x and t, lacks clarity. Hidden information is lurking, and students can be encouraged to problem solve the detail.
The resolution is that the y-coordinates of points D and E have to be equal. This fact was lost when t was introduced in order to avoid confusion over using x with two different meanings. Setting the y-coordinates of D and E equal and substituting for t using step 7 goes like this:
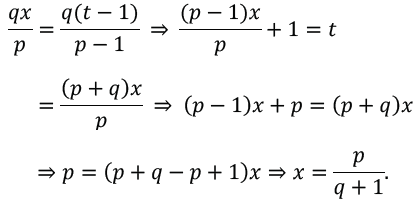
This can then be substituted into D in step 2:
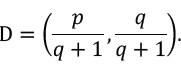
This determines t in step 7:
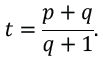
Then, it determines E in step 4:
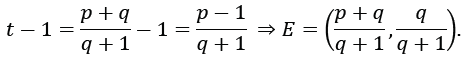
Clearly, this will take far longer than one class. However, keep in mind that I have provided this solution in full generality. Students can choose point C and problem solve with specific values. I have provided the general form here to facilitate using a spreadsheet to verify student work. It can also be used for students to problem solve their own work. To do this, the teacher can provide the formulas, and students can substitute their own values of p and q.
An alternative approach, and the one I prefer, is to have students graph the points they determine so that they can verify graphically if their points make sense. This is shown in Figure 6 for the specific triangle shown in Figure 5.
Students who need enrichment can be asked to determine the area of the square. The simplest way to do so is to use the side length that is the y-coordinate of D and E. The area is
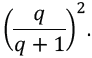
Students can be challenged to explain why this doesn’t depend on p. Given that analytic geometry is relatively new to students, this will help them place a familiar result in a new context. Hints can be given, such as determining whether the base or the height of the square depends on p.
Over the years, I have found that activities like this are beneficial for students. The activity is tiered and allows for different entry points for different students. At the same time, students find that the strategy of mapping out strategic steps separately from completing the calculations in each step is quite effective and
useful. When the process of calculating is combined with the use of dynamic software for checking, students are less apprehensive about the number of steps. As they progress and see themselves achieving agreement between the algebra and the dynamic software, they become increasingly invested in achieving all the steps.
It may interest readers that the inspiration for this particular activity was an unsolved problem in geometry. The inscribed square problem asks whether every closed loop that does not intersect itself has four points that are the vertices of a square. Clearly, this
is true for triangles and, in fact, true for many curves, but it has not been proven for allowable curves.
Timothy Sibbald is an Ontario certified teacher (OCT) and an associate professor in the Schulich School of Education at Nipissing University, in North Bay, Ontario. He teaches in the preservice program and the graduate programs, with a focus on mathematics instruction. He is also the editor of the Ontario Mathematics Gazette, a publication of the Ontario Association for Mathematics Education.