Allison Robb-Hagg
This paper evaluates the effectiveness of Math Talk to communicate mathematical reasoning in French. This high-impact strategy built student confidence and fact fluency in a French immersion context. This action research study, conducted with 19 Grade 4 students, used a mixed-methods approach to examine changes in student confidence as they communicated their mathematical thinking and reasoning. Findings suggested that to increase student confidence and communication of mathematical reasoning, students must collaboratively construct their knowledge. Language frameworks, targeted mental math strategies and established norms were required to cocreate knowledge. Growth in self-confidence in mathematical discourse was p<0.001, indicating a statistically significant time effect, signifying a positive impact on student self-confidence in their ability to communicate their mathematical reasoning in French. This research suggested Math Talk is effective in helping students communicate mathematical thinking and reasoning in a second language learning context.
Punaro and Reeve (2012) found a significant relationship between worrying about math and problem solving in nine-year-old students.
Math trauma and math anxiety are real. As a teacher and as someone who suffered math trauma as a child, I see and feel the impact of mathematical anxiety every day in my Grade 4 French immersion classroom. Students who were once described as confident and competent mathematicians are becoming tentative and reluctant, saying that they are “bad at math.” Punaro and Reeve (2012) found a significant relationship between worrying about math and problem solving in nine-year-old students (as cited in Hill et al 2015). An increase in subject-specific mathematical anxiety results in a lack of confidence among students, which has also been tied to a lack of motivation, and students who have low self-concept are not confident in their mathematical abilities, resulting in poor performance (Organization for Economic Cooperation and Development [OECD] 2014). Mathematical anxiety affects not only conceptual understanding but also students’ social-emotional well-being and mathematical confidence. Student mental health is at risk with the absence of foundational knowledge, jeopardizing their mathematical futures (Dowker, Sarkar and Looi 2016). It was this growing lack of confidence and observed anxiety in the math classroom that led me to conduct an action research project with my students. Action research is a teacher-driven inquiry that responds to a problem of practice. In this case, why are students becoming less confident in communicating their mathematical thinking and reasoning? What can I do about it?
Did their lack of ability to express their mathematical thinking and reasoning affect their mathematical confidence and computational skills?
As a language teacher, the tension between wanting to have students express their mathematical thinking and reasoning while correcting their grammar and vocabulary in the target language is a constant battle. Language learners do not have the necessary vocabulary at their fingertips the way they do in their first language, nor do they always have the correct sentence structure. Teachers are encouraged to prompt and recast to correct mistakes (Lyster and Izquierdo 2009) to avoid solidifying errors; however, this has the potential to interrupt the flow of mathematical thinking, resulting in students getting flustered and giving up.
My school has been focusing on the use of the neurolinguistic approach (NLA) to language acquisition. NLA is a pedagogical approach to acquiring and teaching a second language that focuses on the ability to communicate, with an emphasis on the use of oral language. As a second language school, our students are strong in the use of oral language. I began to wonder how we could leverage this strength in using oral language in math class. Did their lack of ability to express their mathematical thinking and reasoning affect their mathematical confidence and computational skills? I wondered if there was a way to combine our current work in NLA and the high-impact strategy of Math Talks as a way for students to build their mathematical confidence. It was my theory that if you can talk about a concept in the target language, then students will have some level of engagement and understanding, hence building confidence. “The core of mathematics is reasoning—thinking through why methods make sense and talking about reasons for the use of different methods” (Boaler, Williams and Confer 2015).
Barwell (2020) reminds us to consider the added layer of complexity when learning a second language while developing the language of mathematics.
Parker (2019) also suggests students are more eager to learn subject-specific vocabulary when it helps them communicate their thinking more efficiently. A way to do this is with a Math Talk. A Math Talk is a short routine (10–15 minutes) that intentionally designs oral language math tasks that engage students in metacognitive thinking, empowering a culture where learning is cocreated by the students and results in the automaticity of their basic facts (Schoenfeld 1992; Veenman, Van Hout-Wolters and Afflerbach 2006, 148, as cited in Hattie, Fisher and Frey 2017). Research shows that past pedagogical practices such as timed tests and procedural learning create conditions for subject specific anxiety to flourish. This results in a child’s inability to become an autonomous, confident and competent mathematician (Sun 2018); thus, it is important to look at learning conceptually. Barwell (2020) reminds us to consider the added layer of complexity when learning a second language while developing the language of mathematics. This is reflected in my research as this study suggests that engaging in Math Talks builds student confidence by giving them the tools necessary to communicate their mathematical thinking and reasoning in the target language. This research argues the use of Math Talk in a French immersion classroom will increase student confidence, resulting in a decrease in observed mathematical anxiety during math class.
Review of the Literature
Decreased Mathematical Self-Confidence as a Result of Mathematical Anxiety
Mathematical anxiety, a subject-specific anxiety, is a strong physiological and psychological aversion to mathematics, which causes functional changes in the brain including declines in working memory and processing speed (Hembree 1990; Maloney and Beilock 2012; Richardson and Suinn 1972, as cited in Gunderson et al 2018). Mathematics anxiety has been defined as “a feeling of tension and anxiety that interferes with the manipulation of numbers and the solving of mathematical problems in … ordinary life and academic situations” (Dowker, Sarkar and Looi 2016). Mathematical anxiety in the classroom can lead to withdrawal, inattention, fixed mindset and negative attitude resulting in academic decline, but where does the math anxiety come from?
The OECD (2014) results show that math anxiety is influenced by several factors including gender, ethnicity, culture, parents’ views of math, teachers’ anxiety and ineffective pedagogy. All of these variables play a role in identifying possible roots. It is important to identify possible causes and what can be done to potentially mitigate the effects for students.
Math Talk is a high-impact strategy currently being used in many English classrooms to build flexibility, fluency and automaticity with numbers.
Math Talk as an Intervention
Math Talk is a high-impact strategy currently being used in many English classrooms to build flexibility, fluency and automaticity with numbers (Boaler, Williams and Confer 2015). First developed by Ruth Parker and Kathy Richardson, it is intended to allow “every student to find their voice in math class … the beauty of it is that this routine can fully engage every student and every teacher at every level” (Parker 2019, 3). Math Talk returns to the basics of number sense, establishing the foundation for all subsequent work, while providing a psychologically safe environment. Metacognition research shows that students achieve more when they engage in reasoning about their thinking (Schoenfeld 1992; Veenman, Van Hout-Wolters and Afflerbach 2006, 148, as cited in Hattie, Fisher and Frey 2017). Using metacognitive strategies during Math Talk facilitates the students’ ability to struggle productively. For example, students will explain as many ways as possible for mentally solving the problem of 18 × 5 (such as 10 × 5 = 50 and 8 × 5 = 40 then 50 + 40 = 90 or 5 × 5 + 5 × 5 + 5 × 5 + 5 × 3 = 25 + 25 + 25 + 15 = 90 and so on). Students discuss, compare, agree, disagree and analyze the different solutions provided by their peers. Value is placed on the process rather than the answer, which supports productive struggle. A productive struggle is a habit of mind that encourages perseverance and flexibility. Emphasis is put on the process of arriving at the answer (not the product) and the idea that to struggle is productive. This way, for students it becomes about the journey of arriving at the answer and less about finding the right answer. Math talks can “help students learn to embrace the idea of confusion or cognitive dissonance and come to understand that, with mathematics, a state of confusion can be an important and productive place to hang out” (Parker 2019, 6).
When students explain their mathematical reasoning verbally, others understand their process, and all students benefit (Hattie, Fisher and Frey 2017). Research suggests that Math Talk is an effective teaching strategy to increase fact fluency and flexibility to build confidence (Humphreys and Parker 2015). It is yet unknown if this research can be generalizable to second language learning, in this case French immersion, where language is an additional factor.
Implementation of Math Talk in the French Immersion Classroom
Successful implementation of Math Talk requires a classroom community with a mathematical growth mindset where mistakes are valued and productive struggle is embraced. Norms are to be established collaboratively facilitating the positive and supportive culture where students have the psychological safety to be vulnerable. Norms are the set of principles that the classroom community agreed on, which allows a group to work collaboratively. These principles are based on sharing, respect, trust and belonging. Teachers help students to learn to persevere, seeing mistakes as an opportunity in learning rather than a failure (Furner and Berman 2012). One simple yet effective norm, putting up a thumb close to their body rather than putting up their hand, gives students time to think, allowing for all students to participate, regardless of ability. Students who are quick to answer are encouraged to remain silent and to come up with additional strategies, adding a finger up to their thumb for each additional strategy, levelling the playing field between students (Parrish 2011). To facilitate discourse, language frameworks can also be useful as a help to prompt the type of language we want to hear from the students (Hattie, Fisher and Frey 2017). In French immersion, sentence frameworks and posted vocabulary can function as a lifeline for students who otherwise might not participate, serving as a jumping off point for thinking or discussions.
Humphreys and Parker (2015) advise using caution when focusing too intently on the correct sentence structure and use of vocabulary, warning that it may be counterproductive. Focusing on the correct sentence structure, vocabulary and pronunciation, the expression of mathematical reasoning may be hindered, which is especially problematic in a French immersion context. Attention must be given to the balance between intentionality of the lesson (expression of mathematical reasoning) and correction of the language structure.
Research has demonstrated that learning mathematics in a second language is a factor in mathematical performance.
Neurolinguistic Approach (NLA) in Support of Mathematical Discourse
Language acquisition research allows for making a plausible connection between the pedagogical application of Math Talk and teaching math in the target language. “Research has demonstrated that learning mathematics in a second language is a factor in mathematical performance” (Bournot-Trites and Reeder 2001; Clarkson 2007; Ní Ríordáin and O’Donoghue 2009; Secada 1991, 1992, 151, as cited in Barwell 2020). The body of literature focuses primarily on using math talks with English learners, so examining research on language acquisition aids in understanding how mathematical language is acquired.
Netten and Germain’s (2012) NLA paradigm can be examined, and generalizations can be based on what is currently known of the brain and how it processes the acquisition of language. This paradigm explains that language acquisition occurs through implicit and explicit competencies. Implicit competence is the ability to use language spontaneously. Explicit competence is the conscious awareness of how the language works and the structures and frameworks necessary to successfully have knowledge of how the language works. Most important, language acquisition occurs first through oral competence followed by reading and writing (Netten and Germain 2012).
While all of the NLA principles apply, principle five, the need for interplay between students in the classroom, is notable when examining the use of Math Talk in the classroom. NLA research supports frequent use and reuse of oral language in authentic spontaneous communicative situations to build neural pathways to create procedural memory (Netten and Germain 2012). Teachers facilitate language acquisition through modelling and correction of the proper sentence structure and vocabulary. Proper language structures should be encouraged for language to solidify in specific contexts. Using sentence structures and subject-specific vocabulary are essential to student success (Hattie, Fisher and Frey 2017). For example, when students explained their strategy for addition, they used the correct vocabulary (quand j’additionne, la somme est _ parce que… when I add, the sum is __ because) instead of the vague descriptions (this and that is…), which is common when students lack the necessary vocabulary to express their process or reasoning.
Methodology and Theoretical Framework
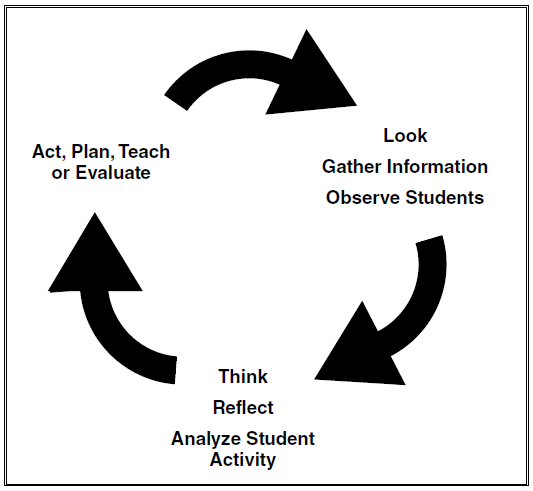
Action research is a systematic method that addresses problems of practice. Grounded in the pragmatist paradigm, action research is iterative in nature and therefore has to be flexible to respond to student needs in the classroom (Parsons et al 2013). This study used both quantitative and qualitative data to evaluate the impact of Math Talks on student confidence and computation. As an action research, this study was teacher-driven and addressed a problem of practice in my Grade 4 classroom. I adhered to Stringer’s (1999, as cited in Parsons et al 2013) simple, yet flexible methodology for conducting classroom-based action research (see Figure 1).
Quantitative and qualitative types of data were useful, adding to the strengths of each perspective while at the same time mitigating their limitations (Creswell 2014). This helped to triangulate the data, enhancing its validity. Quantitative data was collected by having students self-reflect and answer a standard paper confidence questionnaire and self-assessment, which statistically indicated growth of students’ self-confidence over the course of the study. Qualitative data was collected through standard paper student self-assessments, including a rubric asking students to rate their confidence in specific areas such as when talking about math out loud and their thinking and reasoning skills. Students responded with one of three choices: I am there, I am getting there or I am not there yet. Students also commented on things that they did well and suggested an area for growth. Comments provided insight into students’ opinions of their own growth as well as a deeper understanding of the implications for Math Talks in a French immersion classroom and were used to adjust teaching strategies when planning subsequent lessons.
Method
Setting and Participants
This study was conducted with students from a western Canadian Grade 4 French immersion classroom. All students had attended French immersion since kindergarten and were conversational in the French language. All mathematical instruction was conducted in French, while assessments were administered in English. Of the possible 25 students, 19 gave consent; in addition, parental consent was obtained. Thirteen girls and six boys with a mean age of 9.3 constituted the study. No student had participated in a Math Talk prior to participating in this study.
Data Collection
Students were the exclusive source of data collection. The study comprised three phases. All data was collected in students’ first language: English.
Phase 1: Confidence questionnaire was administered to students. Questions included subcategories of motivation, value, self-confidence and enjoyment of math. Students indicated their feelings based on a four-point Likert scale.
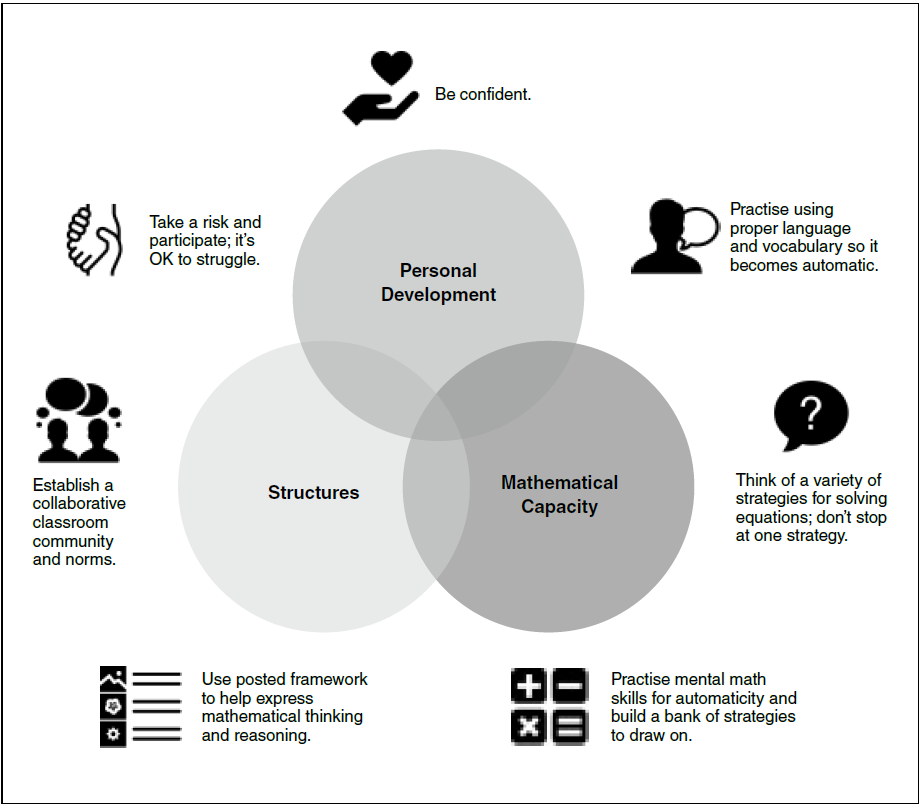
Phase 2: Four Math Talk lessons were administered over two weeks. Students communicated mathematical thinking, reasoned and used mental math strategies. Students completed self-assessments of their level of confidence, which were analyzed after each Math Talk and used to plan subsequent tasks as well as to adjust teaching. Qualitative data and student comments were coded, then grouped and themed. Emerging themes identified by students were grouped into overarching categories of personal development, mathematical capacity and structures.
Phase 3: Confidence questionnaires were administered a second time to compare with the baseline. To meet ethics requirements, a third party collected the data while a school board employee ensured student safety and confidentiality.
All data was anonymized prior to analysis. Limitations of this study include the limited amount of time to conduct the research study resulting in a limit in scope and small sample size, which varied between 8 to 19 participants depending on the Math Talk.
Discussion
Based on the findings of this study and the literature, key conditions are necessary for the successful implementation of Math Talk in a French immersion or language learner context. Highlighted are the three intentional steps to take to successfully impact student self-confidence, resulting in a decrease in mathematical anxiety. In the data collected, students commented that they were building their confidence by developing a growth mindset and engaging in productive struggle. Using the structures provided as well as building their mathematical capacity in computation allowed students to feel more confident in sharing their mathematical thinking and reasoning. The surrounding figures represent the conditions that students indicated were the necessary conditions for success when engaging in a Math Talk in French (see Figure 2).
Beginning by establishing classroom norm and culture that is safe and caring is paramount to the successful implementation of a Math Talk.
Norms and Psychological Safety
A consistent theme throughout the literature, which was supported by the study, is that students require a psychologically safe environment that allows them to take risks and engage in productive struggles. “A situation in which a young language learner feels subject to the ridicule of his or her friends has a strong potential to divert attention to self-protection motives because social acceptance is one of the most salient motives for adolescents” (Olthof and Goossens 2008; Ullrich-French and Smith 2007, as cited in MacIntyre, Burns and Jessome 2011).
Beginning by establishing classroom norm and culture that is safe and caring is paramount to the successful implementation of a Math Talk. An analysis of the students’ self-assessment data after the Math Talks suggested positive growth between the pre and post self-assessment questionnaire for question one: “I feel comfortable talking about math in class.” A statistically significant time effect indicated growth in student confidence over the course of the four Math Talks. These results were supported by the qualitative findings that students had developed mathematical confidence through the use of Math Talks. Students were asked for specific examples of things that they had done well after each Math Talk. Comments for the question, “Things I did well” included, “I told Madame my answer,” “I did well at contributing to the discussion,” “I feel comfortable talking about math in front of the class” (student comments from self-assessment 2018). A review of students’ comments allowed for monitoring of developing self-confidence and fact fluency as well as gained insight into student perseverance (Kersaint 2017) between each Math Talk. The students’ comments also allow for teaching adjustments as well as implementing the required supports. The most important adjustment made during the study was the addition of the posted Math Talk sentence structure framework and posted vocabulary.
Language Framework
As part of the action research cycle, students’ comments were analyzed after each Math Talk for possible improvement and teaching adjustments. The greatest statistical significance during the study was indicated between time two and four, yet there was a statistically significant time effect between the beginning and conclusion of the Math Talk study. This could be attributed to students becoming accustomed to the norms and structures as they were beginning to reason using the French language. By Math Talk four, students were beginning to not only explain their mathematical reasoning in French but were also engaged in a debate about the validity and efficacy of their claims with their peers.
These findings are supported by the research of Humphreys and Parker (2015) that indicates establishing a way of communicating about mathematical thinking not only grows student confidence but also helps them make sense out of mathematics and mathematical relationships. Building a classroom culture based on agreed on norms is essential in providing students with the psychological safety necessary to fully engage in discourse, struggle productively and feel safe enough to publicly contest others.
Following the first Math Talk, students’ comments indicated a lack of confidence when having to discuss and defend their answers. Specifically, students mentioned that they did not have the necessary French vocabulary or sentence structure to express what they were wanting to communicate mathematically. As a result, students coconstructed the visual sentence framework and listed the strategies possible using the correct vocabulary.

In Figure 3, the student will begin by stating the answer. “La somme est _ parce que… (the sum is… because…). The word because is the most important part of this framework as it requires students to explain how and why. In particular, students will explain why they used a particular strategy and will to justify it. The students will then defend their answer using the yellow strips; for example, I used the strategy of…, I rounded, I estimated, I decomposed _ so that I could_. Once the student has finished their statement, their peers are invited to agree or disagree using the green strips: I agree because or I disagree because…, as well as a way to specifically address a strategy used by a peer. This framework allows students to use the correct sentence structure and vocabulary necessary to express their mathematical thinking and reasoning. Using the principles of NLA, it is through the explicit teaching of the mathematical vocabulary and sentence structure that the implicit use of vocabulary and correct sentence structure will arise. Building common mathematical language aids in constructing conceptual understanding as a whole class. It was instrumental to the success of the subsequent Math Talks, and similar frameworks are still coconstructed with students at the beginning of each new mathematical concept.
When examining the pairwise comparison on time effect between times one and three, there was a positive impact on student confidence. However, student comments identified that “using the math vocabulary” and “trying to remember the strategy in my head to talk about it” were still areas for growth in the subsequent self-assessments. Students continued to require the teacher to pay attention to the specific French vocabulary and sentence structure while learning to reason mathematically.
Traditionally, no visible vocabulary or language frameworks are present during a Math Talk or NLA. In the context of this study, however, it was determined that students required additional visual supports that were coconstructed to meet their emerging needs. Once readily available, the students actively used the visual supports to confidently express their mathematical thinking in French. Students indicated through comments that these frameworks were necessary, yet practising using the correct sentence structure and vocabulary was still an area for growth. This was supported by the preliminary data that indicated that greater efficacy could have been achieved with more Math Talks over a longer time.
Do note that “more talk in classrooms does not necessarily enhance student understanding. Better understanding is dependent on particular pedagogical approaches purposefully focused on developing a discourse culture that elicits clarification and produces consensus within the classroom community” (Walshaw and Anthony 2008, 522).
Encourage Productive Struggle and Mathematical Growth Mindset
A mathematical growth mindset is paramount for a successful Math Talk. Self-confidence is an impor-tant factor in mathematics self-concept, which is necessary for a mathematical growth mindset. The mathematical growth mindset is a belief that with hard work and perseverance, anyone, regardless of ability, can succeed in mathematics. Fostered inten-tionally through effective strategies, meaningful discourse occurs when a classroom culture of partici-pation and equitable learning experiences are valued (Bennett 2014). In contrast, fixed mindset, students are unable or unwilling to make the changes necessary to grow, resulting in low self-confidence (Dweck 2006). Implications of low self-confidence could include avoiding mathematical activities and situa-tions, which leads to reduced fluency (Dowker, Sarkar and Looi 2016). Risk-taking acquiesces mistakes and facilitates growth mindset, thereby increasing student confidence. “We now know that when students make mistakes in math, their brain grows, synapses fire and connections are made” (Boaler, Williams and Confer 2015, 5). Students need to know that struggling is productive, and it facilitates deeper learning, which helps students to make connections among mathe-matical relationships. Establishing a culture where mistakes equate to learning is the foundation of hav-ing a mathematical growth mindset (Dweck 2006).
Research shows increasing students’ conceptual understanding in math is essential to math-anxious students’ success (Beilock et al 2004; Ashcraft and Krause 2007; Turner et al 2002, as cited in Boaler 2014; Parrish 2011; Ramirez et al 2013). Although conceptual understanding can be achieved in different ways, one of the more effective methods is through open-ended tasks and practices that value different ways of thinking such as number talks, also known as Math Talks (Parrish 2011; Boaler 2014). Scholars have also observed that math anxiety was higher in classrooms that valued performance over mastery (Turner et al 2002; Ashcraft and Krause 2007, as cited in Boaler 2014).
Over the course of the study, students who self-assessed their confidence using Math Talk suggested positive growth in self-confidence in the area of com-municating their thinking and reasoning. Impact on self-confidence was indicated by analyzed data col-lected from the self-assessment rubric, goal setting and self-confidence subcategory of the pre and post questionnaire. As my position as a researcher was emic, from inside the classroom, I witnessed students increase their use of mathematical vocabulary, mental math, strategies and use of the framework as well as a decrease in observed mathematical anxiety.
Conclusion
Talking about math “can lure students into the world of mathematics and builds their confidence and their beliefs in themselves as sense makers” (Parker and Humphreys 2018, 81). Building self-confidence is the first step to reducing observed mathematical anxiety in the classroom as research has shown that mathematics anxiety impacts basic computation and fluency (Ashcraft and Ridley 2005; Maloney et al 2010, as cited in Young, Wu and Menon 2012) impacting students’ self-confidence in their abilities and therefore their performance.
Math talks are now a daily routine in my Grade 4 French immersion classroom as well as many other classrooms in my school. Supported by visual sentence frameworks and posted vocabulary, students are able to reason mathematically in the target language with confidence and ease. Important to remember is the purpose of the Math Talk by correcting sentence structure or vocabulary in French only if it will not hinder the flow of the mathematical thinking.
After the conclusion of the study, other teachers at my school began to implement Math Talks in their classroom using the planning tools and frameworks developed during this study. We are beginning to see an impact as a school, for example, in the level of excellence achieved by the Grade 6 students during their provincial achievement test (PAT) on the fact fluency component. Post PAT, students reported feeling confident and scored much higher than they had on the MIPI (Mathematical Intervention/Programming Instrument) conducted in September since be-ginning the daily routine of Math Talks. We will continue to use Math Talks and monitor students for long-term effects on confidence and computation.
This study is a beginning for evaluating the impact of Math Talk in a second language context, specifically in French, on student mathematical confidence. More research is needed to study the long-term effects of using Math Talk supported by NLA principles and frameworks. A longitudinal study with more participants is required to examine its full impact and to assess the long-term effects on increasing student confidence in combating mathematical anxiety. Observationally, its efficacy is evident as my students grow in mathematical confidence, mindset and flu-ency. They engage with rigour and enthusiasm in the daily Math Talks, shining with confidence. I highly recommend you give it a try!
Bibliography
Alberta Government. 2014. Handbook for French Immersion Administrators. https://education.alberta.ca/media/3115178/frimmhandbook.pdf (accessed January 18, 2021).
———. 2017. Competencies and the Current Programs of Study Mathematics. https://education.alberta.ca/media/3576122/comp-in-math_20mar_17_final.pdf (accessed January 18, 2021).
———. 2018. Provincial Achievement Test Multiyear Reports. https://education.alberta.ca/media/3772574/pat-multiyearprovince-report-graph.pdf (accessed January 18, 2021).
Alberta Teachers’ Association (ATA). 2000. Action Research Guide for Alberta Teachers. www.teachers.ab.ca/sitecollectiondocuments/ata/publications/professionaldevelopment/actionresearch.pdf (accessed January 18, 2021).
Ashcraft, M H. 2002. “Math Anxiety: Personal, Educational and Cognitive Consequences.” Current Directions in Psychological Science 11, no 5: 181–85.
ATOMIC Teacher. 2016. “How to Do a T-Test for Beginners.” You-Tube video. www.youtube.com/watch?reload=9&v=qvPWQe03tQ (accessed January 18, 2021).
Barwell, R. 2020. “Learning Mathematics in a Second Language: Language Positive and Language Neutral Classrooms.” Journal for Research in Mathematics Education 51, no 2: 150–78, DOI:10.5951/jresematheduc-2020-0018.
Bennett, C A. 2014. “Creating Cultures of Participation to Promote Mathematical Discourse.” Middle School Journal 46, no 2: 20–25. http://dx.doi.org/10.1080/00940771.2014.11461906
Boaler, J. 2014. “Research Suggests That Timed Tests Cause Math Anxiety.” Teaching Children Mathematics 20, no 8: 469–74.
———. 2016. Mathematical Mindsets. San Francisco, Calif: Jossey-Bass.
Boaler, J, C Williams and A Confer. 2015. “Fluency Without Fear: Research Evidence on the Best Ways to Learn Math Facts.” Youcubed website. www.youcubed.org/evidence/fluency-without-fear/ (accessed January 18, 2021).
Calgary Board of Education. 2018. Mathematical Discussion. https://portal.cbe.ab.ca/staffinsite/teaching/learningresources/Mathematical-Discussions.pdf (accessed January 18, 2021).
Cargnelutti, E, C Tomasetto and M Passolunghi. 2017. “How Is Anxiety Related to Math Performance in Young Students? A Longitudinal Study of Grade 2 to Grade 3 Children.” Cognition and Emotion 31, no 4: 755–64. http://dx.doi.org/ DOI: 10.1080/02699931.2016.1147421 (accessed January 18, 2021).
Creswell, J W. 2014. Research Design: Qualitative, Quantitative, and Mixed Method Approaches. 4th ed. Thousand Oaks, Calif: SAGE.
Dowker, A, A Sarkar and C Looi. 2016. “Mathematics Anxiety: What Have We Learned in 60 Years?” Frontiers in Psychology 7, 508.
Dweck, C S. 2006. Mindset: The New Psychology of Success. New York: Random House.
Englebrecht Learned, C. 2016. “Mathématiques en français, Math in English: Discourse in an Elementary School French Immersion Classroom.” PhD dissertation, University of Ottawa https://ruor.uottawa.ca/bitstream/10393/35031/1/Engelbrecht_Learned_Carrie_2016_thesis.pdf (accessed January 18, 2021).
Finlayson, M. 2014. “Addressing Math Anxiety in The Classroom.” Improving Schools 17, no 1: 99–115.
Foster, C. 2016. “Confidence and Competence with Mathematical Procedure.” Educational Studies in Mathematics 96, 271–88.
Furner, J M, and B T Berman. 2012. “Review of Research: Math Anxiety: Overcoming a Major Obstacle to the Improvement of Student Math Performance.” Childhood Education 79, no 3: 170–74. http://dx.doi.org/https://doi.org/10.1080/00094056.2003.10522220 (accessed January 18, 2021).
Government of South Australia Department for Education and Child Development. 2017. “Beliefs and Attitudes About Mathematics.” 1.0 Mathematics, 1–6. www.gaweastps.sa.edu.au/docs/DECD_BEST-ADVICE_1.0_Beliefs-and-attitudes-about-mathematics_v12.pdf (accessed January 18, 2021).
Griggs, M S, S E Rimm-Kauffman, E G Merritt and C L Patton. 2021 “The Responsive Classroom Approach and Fifth Grade Students’ Math and Science Anxiety and Self-Efficacy.” School Psychology Quarterly 28, no 4: 360–73. http://dx.doi.org/DOI: 10.1037/spq0000026 (accessed January 15, 2021).
Gunderson, E, D Park, E A Maloney, S L Beilock and S C Levine. 2018. “Reciprocal Relations Among Motivational Frameworks, Math Anxiety, and Math Achievement in Early Elementary School.” Journal of Cognition and Development 19, no 1: 21–46, DOI: 10.1080/15248372.2017.1421538.
Hartwright, C E, C Y Looi, F Sella, A Inuggi, F H Santos, C González-Salinas, J M Garcia Santos, R C Kadosh and L J Fuentes. 2018. “The Neurocognitive Architecture of Individual Differences in Math Anxiety in Typical Children.” Scientific Reports 8, no 8500: 1–10. www.nature.com/articles/s41598-018-26912-5 (accessed January 18, 2021).
Hattie, J, D Fisher and N Frey. 2017. Visible Learning for Mathematics: What Works Best to Optimize Student Learning Grade K–12. Thousand Oaks, Calif: Corwin.
Hill, F, I C Mammarella, A Devine, S Caviola, M Passolunghi and D Sz cs. 2015. “Maths Anxiety in Primary and Secondary School Students: Gender Differences, Developmental Changes and Anxiety Specificity.” Learning and Individual Differences 48: 45–53. http://dx.doi.org/http://dx.doi.org/10.1016/j.lindif.2016.02.006 (accessed January 18, 2021).
Humphreys, C, and R Parker. 2015. Making Number Talks Matter: Developing Mathematical Practices and Deepening Understanding, Grades 4–10. Portland, ME: Stenhouse.
———. 2018. Digging Deeper: Making Number Talks Matter Even More. Portland, ME: Stenhouse.
Hunsley, J, and S L Flessati. 1988. “Gender and Mathematics Anxiety: The Role of Math-Related Experiences and Opinions.” Anxiety Research 1, 215–24. http://dx.doi.org/ DOI: 10.1080/08917778808248720 (accessed January 18, 2021).
Jansen, A, B Cooper, S Vascellaro and P Wandless. 2017. “Rough-Draft Talk in Mathematics Classrooms.” Mathematics Teaching in the Middle School 22, no 5: 304–07.
Justicia-Galiano, M J, M E Martín-Puga, R Linares and S Pelegrina. 2017. “Math Anxiety and Math Performance in Children: The Mediating Roles of Working Memory and Math Self-Concept.” British Journal of Educational Psychology 87, no 4: 573–89.
Kersaint, G. 2017. Orchestrating Mathematical Discourse: Creating Successful Classroom Environments When Every Student Participates in Rigorous Discussions. https://ttaconline.org/Document/zxbIhX_YCJNP0qvIYsAjT0x-qdzE3VlX/WP-Curriculum_Associates–Orchestrating_Mathematical_Discourse.pdf0.pdf (accessed January 18, 2021).
Lilejdahl, P. 2016. “Building a Thinking Classroom: Conditions for Problem Solving.” In Posing and Solving Mathematical Problems: Advances and New Perspectives, ed P Felmer, J Kilpatrick and E Pekhone. https://portal.cbe.ab.ca/staffinsite/teaching/learningresources/BuildingThinking%20ClassroomsCh1.pdf (accessed January 18, 2021).
Lyster, R, and J Izquierdo. 2009. “Prompts Versus Recasts in Dyadic Interaction.” Language Learning 59, 453–98.
MacIntyre, P, C Burns and A Jessome. 2011. “Ambivalence About Communicating in a Second Language: A Qualitative Study of French Immersion Students’ Willingness to Communicate.” The Modern Language Journal 95, no 1: 81–96.
Morsanyi, K, C Busdraghi and C Primi. 2014. “Mathematical Anxiety Is Linked to Reduced Cognitive Reflection: A Potential Road from Discomfort in the Mathematics Classroom to Susceptibility to Biases.” Behavioral and Brain Functions 10, no 31: 1–13. http://dx.doi.org/https://doi.org/10.1186/1744-9081-10-31 (accessed January 18, 2021).
National Council of Teachers of Mathematics. 2013. “Math Anxiety in Elementary School.” Teaching Children Mathematics 19, no 7, 405–07. http://dx.doi.org/doi:10.5951/teacchilmath.19.7.0405 (accessed January 18, 2021).
Netten, J, and C Germain. 2012. “A New Paradigm for the Learning of a Second or Foreign Language: The Neurolinguistic Approach.” Neuroeducation, 1, 85–114.
Organization for Economic Co-Operation and Development (OECD). 2014. “Mathematics Self-Beliefs and Participation in Mathematics-Related Activities.” PISA 2012 Results: Ready to Learn: Students’ Engagement, Drive and Self-Beliefs 3, 79–104. www.oecd.org/pisa/keyfindings/PISA2012-Vol3-Chap4.pdf (accessed January 18, 2021).
Parker, R. 2019. “How Number Talks Serve Underrepresented Students and Language Learners.” Mathematics Education Collaborative website. www.mec-math.org/ (accessed January 8, 2021).
Parrish, S D. 2011. “Number Talks Build Numerical Reasoning: Strengthen Accuracy, Efficiency and Flexibility with These Mental Math and Computation Strategies.” Teaching Children Mathematics 18, no 3: 198–206. http://dx.doi.org/DOI:10.5951/teacchilmath.18.3.0198 (accessed January 8, 2021).
Parsons, J, K Hewson, L Adrian and N Day. 2013. Engaging in Action Research: A Practical Guide to Teacher-Conducted Research for Educators and School Leaders. Edmonton, Alta: Brush Education.
Ramirez, G, E A Gunderson, S S Levine and S L Beilock. 2013. “Math Anxiety, Working Memory and Math Achievement in Early Elementary School.” Journal of Cognition and Development 14, no 2: 187–202. http://dx.doi.org/DOI:10.1080/15248372.2012.664593 (accessed January 15, 2021).
Saldaña, J. 2013. The Coding Manual for Qualitative Researchers. Los Angeles, Calif: SAGE.
Sherin, M. 2002. “A Balancing Act: Developing a Discourse Community in a Mathematics Classroom.” Journal of Mathematics Teacher Education 5, no 3: 205–33.
Stuart, V B. 2000. “Math Curse or Math Anxiety?” Teaching Children Mathematics 6, no 5: 330–35. www.jstor.org/stable/41197431 (accessed January 15, 2021).
Sun, K L. 2018. “The Role of Mathematics Teaching in Fostering Student Growth Mindset.” Journal for Research in Mathematics Education 49, no 3: 330–55.
Tang, M. 2008. “Student Use of Language in French Immersion Mathematics.” Master’s thesis, Simon Fraser University. http://summit.sfu.ca/item/9294 (accessed January 15, 2021).
Varol, F, and D Farran. 2007. “Elementary School Students’ Mental Computation Proficiencies.” Early Childhood Education Journal 35, no 1: 89–94. http://dx.doi.org/DOI: 10.1007/s10643-007-0173-8 (accessed January 15, 2021).
Vukovic, R K, M J Kieffer, S P Bailey and R R Harari. 2012. “Mathematics Anxiety in Young Children: Concurrent and Longitudinal Associations with Mathematical Performance.” Contemporary Educational Psychology 38, no 1: 1–10.
Walshaw, M, and G Anthony. 2008. “The Teacher’s Role in Classroom Discourse: A Review of Recent Research into Mathematics Classrooms.” Review of Educational Research 78, no 3: 516–51. http://dx.doi.org/DOI:10.3102/0034654308320292 (accessed January 15, 2021).
Young, C B, S S Wu and V Menon. 2012. “The Neurodevelopmental Basis of Math Anxiety.” Psychological Science 23, no 5: 492–501. http://dx.doi.org/https://doi.org/10.1177/0956797611429134 (accessed January 15, 2021).
Yüksel-Sahin, F. 2008. “Mathematics Anxiety Among 4th and 5th Grade Turkish Elementary School Students.” International Electronic Journal of Mathematics Education 3, no 3: 179–92. www.iejme.com/download/mathematics-anxiety-among-4th-and-5th-grade-turkish-elementary-school-students.pdf (accessed January 15, 2021).
Allison Robb-Hagg is a Grade 4 teacher with the Calgary Board of Education and a sessional instruc-tor with Ambrose University. Her research areas include online preservice teacher development and teaching mathematics in a second language context.






