Josh Markle
In this paper, I recount using the Fu-Go program, an offensive launched by the Japanese Navy in World War II, as a provocation for mathematical inquiry in the classroom. Drawing on my experience as a secondary mathematics teacher in an alternative high school, I suggest some ways case studies such as this can be used to foster rich conversation and develop a disposition of expertise in the mathematics classroom.
Introduction
It is dawn in early winter 1944. At the outskirts of a small town on Japan’s eastern seaboard, members of the Japanese Navy are assembled to launch one of its most cunning attacks of World War II. Lifting off Japan’s coast into the cool morning light are a half-dozen balloons, each laden with incendiary de-vices and destined for the US mainland. It would have been a sight to behold: each balloon was approximately 10 metres in diameter with a volume of nearly 19,000 cubic feet (Mikesh 1973, 40). Appended to the bottom was a series of altimeters, each connected to a fuse designed to release sandbags along its trans-Pacific flight. If a balloon’s flight went according to plan, ordnance intended to ignite wildfires and sow panic in the American populace would follow the last of the sandbags. This was Japan’s Fu-Go weaponized balloon program.
Although the program, named Fu-Go after the Japanese word for balloon (fusen), was conceived in the late stage of World War II, Japan’s experimentation with balloons dates back much earlier. Decades prior, a Japanese meteorologist, named Wasaburo Ooishi, used small weather balloons to collect data showing wind speeds in excess of 260 kilometres per hour. Perhaps most important, Ooishi established a definite pattern in the seemingly capricious winds that blew high above the island: they were seasonal, blowing far stronger in the winter months, and were relatively stable at high altitudes, between 30,000 and 35,000 feet. This was the reason for the complex apparatus appended to the balloon’s undercarriage: as the hydrogen inside the balloon’s paper envelope cooled and heated along its flight path, it was necessary to cut weight or vent gas in order to stay within the strong wind currents. If successful, Japanese meteorologists were able to establish a trans-Pacific flight time of 30 to 100 hours.
Looking at Fu-Go in the Mathematics Classroom
I have used Fu-Go both as primary material for an assignment in high school mathematics classes and as a lesson planning provocation in my work with preservice math teachers in their curriculum and instruction courses, all to great effect. In the former case, I taught Math 20-2 and 30-2 at an alternative high school in a small, western Canadian city. My classroom was diverse. There were students who had already graduated high school but were upgrading, who were taking this course to meet the requirements of a postsecondary program and who had had to leave classrooms in their home schools for myriad reasons, such as low achievement and poor attendance. Though diverse, the students were generally bound by one commonality: they had all experienced a lack of success in the mathematics classroom.
The “dash-2” Alberta mathematics curriculum allows for considerable depth and breadth. In addition to outcomes oriented around particular mathematics, such as quadratic functions, the Math 20-2 and 30-2 curricula require students to engage in a mathematics research project. Specifically, students must research a historical event or area of interest (Alberta Education 2008, 27). There are many opportunities to incorporate history into mathematics, in particular the history of mathematics itself. Fauvel (1991) makes a compelling case for including the history of mathematics in teaching mathematical concepts. Panagiotou (2011) describes doing so in teaching logarithms in the secondary classroom. In this case, we looked not so much to a particular historical development in mathematics, but rather what a historical event might reveal to us about our current understandings of mathematics, in particular quadratic equations.
Although it is common to tackle this kind of re-search project toward the end of the semester, several factors made this difficult in our context. As noted above, the students I worked with often experienced difficulty in attending regularly and frequent disruptions in their coursework. To compound this, our class was structured so that students could work at their own pace on several of the course’s components. Although convenient for many students, this aspect of the course made it difficult to implement a large final project. To mitigate this, I curated a small selection of historical events and areas of interest that we could investigate as a class as we proceeded through the curriculum. The Fu-Go project was one of the most engaging and effective.
There are two texts indispensable in knowing more about Fu-Go. Mikesh (1973) is closer in nature to a technical manual and is full of schematics and maps; Coen (2014), also thorough in its detail of the pro-gram, better captures the social contexts of the American and Canadian responses to the attacks. Both are excellent resources. But perhaps the most accessible and engaging treatment of the topic is an hour-long RadioLab podcast (Abumrad and Krulwich 2015). In my work with both high school students and preservice teachers, this podcast is our primary text. In both instances, I allot time in class to listen to the podcast. Students are required to listen through headphones and are given instructions to note anything of interest to them while they listen. Instructional time is always at a premium, but I chose to allocate an hour to listening because I wanted to provide an immersive experience in which students could dwell, notice and wonder. It was also beneficial to begin discussing the material immediately afterward in class.
After listening to the RadioLab episode, we took time to organize our thoughts individually using the following prompts: What do you notice? What do you wonder? This gives students time to organize their notes, to go back to the episode and listen to parts that intrigued or confused them, and it gives me an opportunity to visit briefly with each of them. Once we felt confident to share our insights, we arranged ourselves into small groups to share briefly before having a large group conversation in which all noticings and wonderings are committed to the whiteboard. The students I have worked with have been unfailingly perceptive. Their observations range from logistic (for example, flight path, construction materials) to technical (for example, number of sandbags, mechanics of the altimeters) to emotional (for ex-ample, loss of life). They were equally insightful in their wondering. This included the questions below:
- What and where is the jet stream?
- What factors most influenced flight times?
- What is the farthest a balloon could travel?
- What is the highest a balloon will float?
- Why paper?
- How many balloons made it to the United States?
- What resources did it require to build a single balloon?
To be sure, one wondering always emerges quick-ly: What does this have to do with math class? And it is a legitimate question, one I believe we sufficiently answer in how we attend to the problem. The first step is deciding as a class which noticings and wonderings from our lists are mathematical in nature. Because I use this material as part of our work around quadratic functions in Math 20-2 and sinusoidal functions in Math 30-2, I am most interested in identifying those noticings and wonderings associated with the parameters in those functions, such as the general shape of the flight path, maximum and minimum heights, distance and duration.
A Provocation and Some Possible Solutions
Once we have begun to characterize the nature of our inquiry as mathematic, I offer students the following provocation: How might we describe the flight path of a balloon across the Pacific using what we know about quadratic equations? I have students begin my eschewing mathematical convention and simply drawing. Then we begin to question some of the assumptions in their drawings and how we might be able to characterize these assumptions mathematically. For example, students will often note that the balloon must undulate along its flight path and that the peaks and valleys must represent the upper and lower bounds of the jet stream, respectively. If we interpret this in the context of quadratic equations, this gives us valuable information. Consider a quadratic function in vertex form: f(x) = a(x−h)2 + k
In this form, we know that the vertex is given by (h, k). Assuming the upper bound of the jet stream is 40,000 feet, we can assign a value to k of 40,000.
Then we must consider the time at which a balloon reaches its maximum height (h). Students can make any assumptions they like, provided they are mathematically and physically sound. For example, if a student wants to model a balloon flight to Detroit, they need to make sure their assumptions regarding the flight’s duration accurately reflect the distance travelled and the balloon’s velocity, each another layer of assumption that requires research, critical thought and discussion. Generally, we first discuss these assumptions as a large group and establish some bench-marks. For example, we typically assumed the jet stream to be between 30,000 and 40,000 feet and a typical flight to the US mainland to take 72 hours (a roughly 7,500-kilometre flight at somewhere around 100 kilometres per hour). After some play with the parameters and discussion, I will ask students to provide three quadratic equations that reflect the assumptions we agree on (for example, maximum height, duration of flight)—this gives students a good opportunity to talk with each other and for me to talk with each of them. Figure 1 show the graphs of three such quadratic equations, with the equation for the second parabola in green.
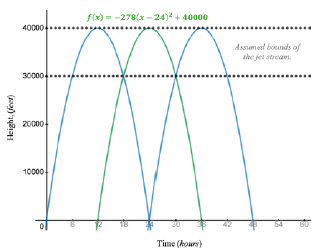
Note: A series of three quadratics show the hypothetical path of a Fu-Go balloon (the portions of the quadratic graphs between the two dotted lines). In discussing the limitations of quadratics for modelling this sort of problem, we focus on the “sharp” corners at the bottom of the low points of the travelled path.
In my formative assessment, I am most interested in understanding whether students see the connection between the function’s parameters and horizontal shifts of the function’s graph. Once I am confident a student has developed a sound understanding of the material, I provide each of them with a unique set of constraints they need to satisfy with a set of three quadratic equations. Constraints might include duration of flight, minimum or maximum number of drops along the flight path, minimum or maximum height, a specific location, specific velocities and so on. Students then present their work, which allows us all to gain further insight into how manipulating a quadratic’s parameters affects its graph.
Mathematizing Conversation
In attempting to contextualize quadratics and parabolas, test and assignment questions often resort to situations that are accessible if prosaic, such as throwing a ball or calculating revenue. But we know that quadratics do not perfectly model either of those situations and Fu-Go is no different. The most rewarding aspect of using this material is the rich conversation it generates in class, both mathematic and otherwise. We always made sure to discuss the benefits and limitations of the assumptions we made. By the end of the investigation, students appreciate that quadratic functions are neither the tool with which the Japanese modelled the attack nor the best means to describe the flight path in hindsight. The point is not to recapitulate the development of the balloon or accurately describe its flight path, but to investigate the parameters of a particular class of functions (for example, quadratic, sinusoidal) in order to develop a more robust and intuitive understanding of their constituent elements and how each of the parts affects the whole.
Our discussions outside of the mathematics were also poignant. One interesting aspect concerns the asymmetry in Japanese and American intelligence and is drawn from the two most comprehensive accounts of Fu-Go. Mikesh (1973) notes that the notion of trans-Pacific balloon travel was a given for the Japanese. Officials there were more concerned with the parameters of flight: at what altitude should they travel? When and where should they be dispatched? (p 7). This contrasts the initial response by American authorities when they began collecting evidence of the attacks on US soil. As Coen (2014) writes, officials first theorized that the balloons were being launched from submarines just off the US coast. “There is no question about it,” he quotes one US intelligence officer as saying, “[the balloon] couldn’t have come from Japan” (Coen 2014, 56). One important reason for incorporating history into the mathematics classroom is to cultivate an appreciation for the reticulated nature of the development of mathematical and scientific thinking across time and cultures.
And although Fu-Go was unsuccessful from a military standpoint, it still had a profound impact. In 1945, a woman and five children were killed when they came upon unexploded ordnance beneath a balloon envelope while on a picnic in Washington state (Coen 2014, 2). According to Mikesh (1973), 17 bombs were confirmed to have landed across Alberta and nearly 40 were located in British Columbia (p 77). One balloon was found in British Columbia as recently as 2014 and there is a good possibility there are others unaccounted for (Abumrad and Krulwich 2015). We drew on many different ideas and fields in our discussions, such as ethics, geography and probability. These discussions belied the idea that mathematics is a collection of unrelated and unrelatable facts. Rather, it is enmeshed with and inextricable from lived experience—a rich source of inquiry and conversation in the math classroom.
References
Abumrad, J, and R Krulwich. 2015. Fu-Go. Audio podcast. RadioLab www.wnycstudios.org/story/fu-go (accessed February 5, 2021).
Alberta Education. 2008. Mathematics 10–12 Program of Studies. Edmonton, Alta: Alberta Education.
Coen, R. 2014. Fu-Go: The Curious History of Japan’s Balloon Bomb Attack on America. Lincoln, Nebr: University of Nebraska Press.
Fauvel, J. 1991. “Using History in Mathematics Education.” For the Learning of Mathematics 11, no 2: 3–6.
Mikesh, R C. 1973. Japan’s World War II Balloon Bomb Attacks on North America. Washington, DC: Smithsonian Institution Press.
Panagiotou, E N. 2011. “Using History to Teach Mathematics: The Case for Logarithms.” Science and Education 20, 1–35.
Josh Markle is an instructor in the Faculty of Education, University of Lethbridge, and a doctoral student in the Werklund School of Education, University of Calgary.






