Lisa Brooks and Janet Andreasen
It is said that money makes the world go round. While that may be debatable, what is clearer is that Grades K–12 students likely have different experiences with money than what most of us teachers had when we were growing up. This presents unique challenges to our instruction. In an effort to address these challenges, we will explore how to simplify the complex topic of money and provide meaningful ways to make connections between money concepts and other topics in mathematics. We will start by focusing our attention on coins.
The use of a structure that moves from concrete to representations and finally to abstract.
When was the last time you used coins in exchange for a purchase? We are guessing that this may not be a regular occurrence. Since the creation of checks and then credit and debit cards, not to mention Venmo, PayPal and so on, our experiences with coins, and money in general, have changed. Now think about the students we teach. Do they have experiences on a regular basis with money or, more specifically, with coins? Chances are, when students arrive in your classroom, they do so without the foundational understanding of coins and their values. So then, how and why do we teach these skills? Perhaps, more important, how do we help students make personal connections to coins and their values and use them to develop a deeper understanding of number sense in the process?
One important aspect that helps students make personal and meaningful connections to a concept is the use of a structure that moves from concrete to representations and finally to abstract (CRA) (Fyfe, McNeil and Borjas 2014). One must remember this sequence when the goal is to build understanding. Students need tangible experiences to make meaningful connections to concepts (Heibert et al 1997). Considering coins as necessary concrete items is logical; however, they do not provide the components we look for regarding concrete items. Each coin represents a value. This is different than base-10 blocks, for ex-ample. Consider the concrete manipulative we use when teaching our base-10 number system. Base-10 blocks provide a concrete model that directly shows ones, tens and hundreds. They allow students to make sense of the 10-to-1 relationship between individual units and 10 rods. Students can physically count out ones until they determine that they can trade 10 ones for a 10 rod. They can line up 10 ones to be the same length as one 10, so they can visually see the connection between the place values. This supports the students as they learn to unitize, that is, to view a 10 as a unit in and of itself as well as a set of smaller units. Later, they may draw representations of the blocks and then, finally, they are able to use a numerical representation of the blocks. The numbers would be considered abstract. Let’s consider how coins are different and therefore not as concrete as we might recognize.
The one-cent coin has been taken out of circulation, but we still need to think of its value in relation to the other coins. Let’s think about the next value of the coin. The nickel, while a tangible item, is not a concrete tool for understanding its value of five cents. The dime, which is worth ten cents, is actually smaller than the nickel, further confusing the matter. When students hold a nickel or a dime, it is likely that their names will not come easily, because their names don’t offer any indication of five or ten. So, while actual coins or plastic coins have a place in the classroom and in instruction, they are not a helpful starting place in regard to building personal connections and meaning related to the value of coins.
Now, let’s consider how we might relate money concepts to number sense. The purpose in doing so is to capitalize on what students are working toward in regard to understanding the relationships between values such as 5, 10 and 25, and to help students make connections between these concepts and the work they do with coin values.
When and How to Teach Money Concepts
It may be difficult to consider when and how to teach money concepts when they are not explicitly stated in the mathematics standards for your grade level. It may also seem necessary to hold off on teaching about coins until students have had the opportunity to develop number sense. We believe you can effectively teach both concepts at the same time. In fact, by bringing in concepts of coin values, you bring meaning and purpose to both skills. In a sense, you give students the opportunity to make more connections to model numbers in various ways. This can help them build their sense of number while also building an understanding of coins.
Starting as early as kindergarten, students can use coins for counting.
One step toward intentionality is to explore the standards indirectly related to money. Table 1 pro-vides examples of typical mathematics standards that can be connected to work with money concepts. They are nonspecific to any particular region and are likely found in your mathematics standards. These standards can help your students to build a foundation of number sense and operations that they may then be able to apply to their work with money. Students will benefit from explicit connections being highlighted during instruction.
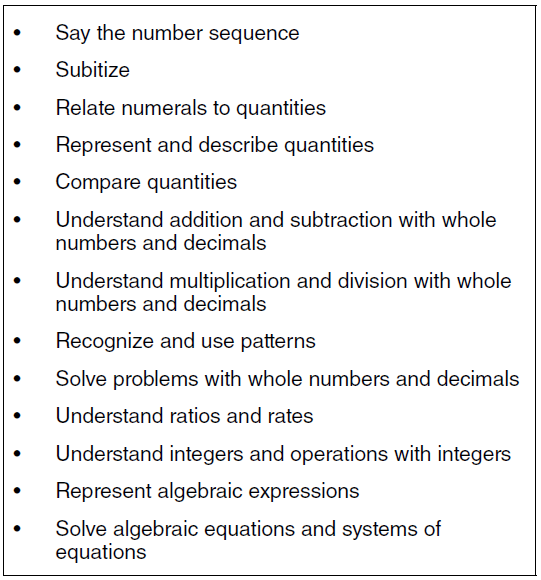
Notice that initially students are benefiting from meaningful connections to build understanding. Later, they extend these connections as they make sense of problems related to money. When you teach related standards, it is appropriate to use coins even though they are not specifically stated in the standards. For example, starting as early as kindergarten, students can use coins for counting. Assuming you can find a collection of 1-cent coins, students can use them to fill in five frames and ten frames to explore one-to-one correspondence, matching and comparing. They can even explore concepts related to equivalence. Stu-dents can also explore showing values in different ways using a variety of coins. They can use frames to show and combine coins up to 20 cents. Later, they can work with multiple frames up to the value of 100 cents. Collections of nickels and dimes can be useful for providing experience in skip counting while, at the same time, reinforcing the value of the coins.
Coins and number frames provide a context that students can use as they learn the value of coins. For example, when you provide students with experiences working with a five frame and then a ten frame, they learn to use these amounts. That is, they learn to see a complete frame and recognize that amount as a unit of five or as a unit of ten as opposed to only five ones or ten ones (Fosnot et al 2001). As they develop this skill, they are making connections to the values of the coins, and they are deepening their concept of unitizing. The more intentionally we address these concepts, the more likely our students are to build understanding and to have a framework for applying flexible thinking about money concepts as well as number sense.
Money Sticks
Linking coin concepts to number sense is helpful, but students may also benefit from having a concrete model to use during instruction. In an attempt to make the coins more tangible and concrete, we can use a model called money sticks (Brooks 2017). This model may help your students make connections with what they are learning in regard to number sense. It also provides an experience that sets the stage for working with different combinations of coins. “Money Sticks are a helpful tool for bridging the gap between a tangible representation of a number and the more abstract idea of recognizing the values of coins” (p 174).
To make this model, you will need wide craft sticks, copper-coloured paint, a circular paint dobber (or anything that will transfer a small paint circle onto the craft sticks) and a collection of the coins you wish to use. How to make the money sticks: make five evenly spaced copper-coloured circles on one side of as many sticks as you would like to create. Each stick will become a concrete representation of a nickel (see Figure 1).

What you do from that point is up to you, your imagination and your students’ needs. You might start by simply having the students practise their counting skills by using one-to-one correspondence to count the dots on the stick. You can use this basic model just as you would a five frame. Students could also work on developing the skill of using one-to-one correspondence as they place a penny on each circle. They could use this model as they would use a five- or ten frame to model different numbers. Later, they can use multiple sticks to work on skip counting. You can decide to focus first on the copper dots as ones and fives, or you can talk about them as ones and pennies while also calling the stick a five and a nickel. To move from identifying the value of five to working with coins, we can replace the copper dots with pennies, and we can also secure a nickel on the back of the stick as shown in Figure 1.
Once students are accustomed to seeing the actual pennies on the stick, the copper dots will suffice for a representation of pennies. The nickel taped to the back of the stick provides the abstract representation of five, and if students forget the value of the nickel, they can flip the stick over and count each of the cop-per penny dots. Students may count several nickel sticks together and again, while counting, if they lose track, they can easily flip the sticks over for the needed support of counting by ones. You could also include the coin names in written form on a small piece of paper or label each side with the value of the coins. So, you might have the word form nickel and five on the back of a money stick to serve as a reminder to the word and value of the coin.
To highlight the connection of the relationships between the coins, use packing tape to secure two sticks together and include a dime on the opposite side (see Figure 2).

If you create a collection of sticks, you can include values of 5s, 10s and 25s. Students could then com-bine sticks to show the value of a greater coin (see Figure 3).
For example, students may model 25 cents using five sticks that have been taped together and then explore other combinations to model 25 cents, such as two 10-cent sticks and one 5-cent stick (see Figure 4).


Using clear packing tape creates a flexible model. Holding the model of five sticks taped to show the value of a quarter, you can fold four of the sticks toward the back and see that you have the value of one nickel facing forward with the other sticks facing to the back. This provides a way to see how the sticks work together to create the total value. Students can apply the same reasoning they use when composing and decomposing numbers to compose and decom-pose different amounts of money.
To engage students in problem solving, have them find different combinations for a given amount. This can be an open-ended task or you can include such limitations as the number of coins they can use. Stu-dents can create questions and share with others to solve. They can also show you how they can model a given amount with the fewest number of sticks or the greatest number of sticks. For example, they can model 50 cents with two quarter sticks or with 10 nickel sticks. You can also ask students how many different values they can make with four sticks. Re-member to have students flip the money sticks so they are looking at the groupings and not the individual penny dots.
Money sticks are likely to be a helpful tool to solidify students’ understanding of numbers and of the value of coins. As students progress in their understanding of both number and coin values, the sticks can be replaced with actual coins and abstract representations of numbers. The foundation they build with this model in the early years can be ap-plied when they are required to use sophisticated strategies for thinking about money in the secondary grades. As students transition to upper elementary grades and high school, the actual coins become less critical to use, and the application of problem solving to money increases. The importance of students’ understanding of the value of coins, however, does not diminish. The money sticks can continue to be used in modelling operations with whole numbers including repeated addition to find the value of multiple sets of particular coins. For example, students may be asked to determine the value of a specific number of quarters. The money sticks can be used here to repeatedly add the quarters and then to model multiplication with groups of objects. Additionally, problem-solving situations can be presented to students involving coins using the context of allowance.
Jennifer gets an allowance of 85 cents per week. What different combinations of coins could Jennifer’s parents give her each week?
Later, students begin to explore ratios and rates. An understanding of money is not a critical component when learning these concepts; however, in addition to other rich contexts, providing contextual problems situated with money can help students make sense of ratios using cents. Likewise, when they encounter situations, either within word problems or in real life, a solid grasp of money concepts will be beneficial. For example, students may be asked to compare the value of a candy bar given a size and cost.
A candy bar that weighs 8 ounces costs 42 cents. A candy bar that weighs 12 ounces costs 65 cents. Which candy bar is the better deal?
If students are lacking understanding of coins and money, these types of situations may be difficult. Students ultimately reason with unit rates and need to understand that the most common rate in this case is cost per ounce, or cents per ounce.
As learning transitions to algebraic reasoning, the situations often will involve money and will connect to rates and repeated addition. For example, students may encounter attending a local fair where it costs $5 to get into the fair and $2 per ride. Students should be able to use their knowledge of money, repeated addition and rates to determine that $2 per ride is the multiplicative factor in the equation. Additionally, using unit analysis helps students see that they need to multiply the rate (dollar per ride) by the number of rides to get the cost. Since the cost to get in ($5) is in dollars and the total cost (C) is dollars, the cost for the rides (2R) should be in dollars as well. This generates an equation like C = 2R + 5 where C is the cost of attending the fair and R is the number of rides. Students then explore this scenario using tables, graphs and equivalent equations. This can then be connected to further algebraic ideas of systems of equations. Take the local fair situation and extend the model to two equations.
The fair has child tickets and adult tickets. Child tickets cost $4 and adult tickets cost $6. A family bought 6 tickets and spent $36. How many child tickets and how many adult tickets did they buy?
Students’ understanding of coins and money can be used to support mathematical reasoning throughout the grade levels.
As students explore this context, they use their knowledge of money and rates. They need to reason that if each child ticket costs $4, the cost of C child tickets would be 4C. Likewise, if each adult ticket cost $6, the cost of A adult tickets would be 6A. Combining these together would give the total money spent to get into the fair, in this case $36. This gives an equation of 4C + 6A = 36. This isn’t enough to solve this system, however, since there are two unknowns. The situation also indicates that the family bought 6 tickets. Here students need to recognize that A and C are the number of each type of tickets purchased, so C + A = 6. Once the students reason through determining the equations, they can then explore the solution using tables, graphs and algebraic methods.
Students’ understanding of coins and money can be used to support mathematical reasoning throughout the grade levels. It provides meaningful context for developing number sense and an understanding of the value of the coins, using the context of money and coins in problem solving related to operations with whole numbers, reasoning about rates and ratios, and connecting algebraic contexts to situations involving money. When we focus on student under-standing, we provide the means for them to make meaningful connections. It is our hope that you find these strategies helpful as you support your students in making sense of money.
Bibliography
Brooks, L A. 2017. “Making Sense of Cents.” Teaching Children Mathematics 3, 170.
Fosnot, C, M Twomey, A Ludovicus and M Dolk. 2001. Young Mathematicians at Work. Portsmouth, NH: Heinemann.
Fyfe, E R, N M McNeil and S Borjas. 2015. “Benefits of ‘Concreteness Fading’ for Children’s Mathematics Understanding.” Learning and Instruction 35, no 2: 104–20.
Heibert, J, T P Carpenter, E Fennema, K C Fuson, D Wearne, H Murray, A Oliver and P Human. 1997. Making Sense: Teaching and Learning Mathematics with Understanding. Portsmouth, NH: Heinemann.
Weiland, L. 2007. “Experiences to Help Children Learn to Count On.” Teaching Children Mathematics 14, no 3:188–92.
Lisa Brooks is an associate lecturer in the College of Community Innovation and Education at the University of Central Florida. Her research focuses on helping teachers facilitate student discourse to increase conceptual understanding of mathematics. She is an experienced elementary and middle school teacher, internship supervisor and coordinator, new teacher mentor, and mathematics coach. She is coauthor of Making Sense of Mathematics for Teaching Grades K–2 (2016) and Making Sense of Mathematics for Teaching the Small Group (2018) and provides professional development for educators, school leaders and district leaders. Brooks earned a bachelor’s degree in elementary education, a master’s degree in mathematics and science education, and a doctorate degree in curriculum and instruction, with a focus on mathematics education.
Janet Andreasen is an associate lecturer of mathematics education at the University of Central Florida (UCF). She is the coordinator of secondary education and works with prospective and practising mathematics teachers at the elementary, middle and high school levels. Andreasen’s research interests include examining mathematical knowledge for teaching and using technology to foster student learning of mathematical concepts. Andreasen received a bachelor’s degree in biomedical engineering from the University of Miami (FL) and both a master’s degree in mathematics education and a PhD in education, mathematics education from the University of Central Florida.