Nicole Langevin, Miwa A Takeuchi, Jenny Yuen and Shayla Jaques
Attention to science, technology, engineering and mathematics (STEM) education has been rapidly growing nationally and internationally (Sengupta, Shanahan and Kim 2019; Takeuchi et al 2020). In Alberta, STEM is not yet a curriculum subject in it-self, although related pedagogical efforts—such as makerspace and design-based learning—are being taken up in Alberta schools.
STEM is a relatively recent domain of studies in the education field. In the EBSCO Academic Search Complete database, the term STEM first appears in education journals from the early 2000s. Since then, the number of publications on STEM education re-search and teacher development resources for STEM education has significantly grown.1
Despite this growth, there is a scarcity of research on STEM education in the early years (kindergarten to Grade 3), compared with the research on secondary and postsecondary STEM education, which could be partially a result of the implicit research agenda of preparing students as future workers for STEM industries (Takeuchi et al 2020). An aesthetic vision for STEM education that centralizes seeing more and seeing the complex (Farris and Sengupta 2016) stands apart from those instrumental visions focusing mainly on workforce preparation. Aesthetic expansion through STEM education enables learners to make familiar phenomena unfamiliar and to notice previously unnoticed elements and meanings in those phenomena. What does STEM education in the early years look like when the teacher aims for aesthetic expansion?
This article sketches a scene of students seeing more in geometry through an early STEM class in Alberta, designed by the mathematics and STEM learning leader at the school. All students in the school experienced a one-hour STEM class twice per week. The teacher arranged the classroom space (by removing individual desks and seats) so that students could move their bodies freely. The classroom housed commercial resources (such as Lego Mindstorms robotics kits, Sphero robots and Ozobot robots), and the teacher also created a free makerspace with a collection of recycled materials (Figure 1). The teacher actively used the classroom wall and the hallway to document and demonstrate the process of the students’ projects, highlighting the design cycle (Figure 2). The final iterations of the students’ creations, as well as their initial plans and photos of the process, were included.


students’ work.
The school was located in a neighbourhood with many apartment buildings, where many recently arrived immigrant and refugee families had settled. Approximately 90 per cent of the students were identified as English-language learners, with various home languages.
In this article, we demonstrate how students in a Grades 1/2 combined class learned key mathematics concepts in this STEM classroom by describing the students’ learning during the final project of the year. The students received two STEM classes per week, and this project took place over six weeks. We will focus on two students, Alex and Hakim, who were both newly arrived students and whose first languages were not English.2 We videotaped classroom interactions over six instruction days and repeatedly re-viewed the videos. We identified the trajectory of engagement by Alex and Hakim as illustrative of the learning that was happening in this STEM class.
In the final project, the students created an art piece with geometric shapes that they had been learning, using Sphero robots as paintbrushes. Each phase of this project presented unique mathematical learning opportunities, as demonstrated in the following sections.
Understanding Polygons Through Coding
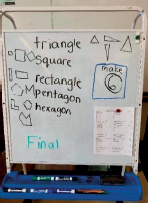
In many early mathematics classrooms, students explore polygons by describing, sorting and comparing provided shapes. In this interactive STEM class-room, the teacher started by challenging the students to draw various polygons based on their definitions. Figure 3 is the teacher’s sketch of the shapes students drew (through gestures). Not only did the students recognize the regular hexagon shape, but they also drew two other shapes that, by definition, are both valid hexagons (six-sided polygons). Many of the students’ existing understanding was based only on exploring regular polygons, such as those found in pattern blocks. As a class, they explored the idea that any closed shape with six sides is a hexagon, even if the sides are not equal.
The students’ understanding of regular and irregular polygons was continually facilitated as they thought about how to code a polygon. After free exploration with Sphero robots and graphing software that tracked the movement of the Sphero, students engaged in discussion about how to code a polygon, as seen in the following interaction:
Teacher. Some triangles have all equal sides, and some triangles are really pointy and long and skinny. Some triangles have some big corners and some small corners. Some triangles point this way or this way. (Gestures her hands toward two different sides of the room.)
Student. Triangles can go in any way!
Again, Figure 3 shows that the students were aware that even triangles can have different angles and direc-tions. The teacher then showed them an example of code with three blocks, as shown in Figure 4.
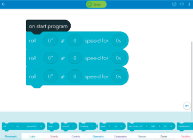
The following interaction shows the student’s understanding that there must be three blocks of code for a triangle, because a triangle has three sides:
Teacher. If I’m making a triangle, why did I start with putting three blocks of code?
Student. Because the triangle has three blocks. Teacher. Has three . . . ? Do you remember what we call those? (Makes a triangle with her hands and uses her right index finger to draw along the side of the triangle on her other hand.)
Student. Has three sides.
In this interaction, the teacher brought the student’s attention to a mathematical term—side. However, instead of correcting the language the student used (blocks), the teacher amplified the linguistic cues with gestures to facilitate fuller student participation in the linguistically diverse classroom, as discussed by Takeuchi and Dadkhahfard (2019).
After this class discussion, the students worked in pairs to code the Sphero robots to roll in the shape of polygons of their choice. By the next class, Alex and Hakim had successfully made two quadrilaterals and a triangle. After this practice with the programming language, they challenged themselves by attempting to create a more difficult shape—a pentagon.
They started with five blocks of code for the five sides of a pentagon and programmed angles, speeds and time (all seemingly guesses) into the code. After their first test, they noticed that the Sphero had made an L shape, not a closed shape like they wanted. They decided to increase the numbers on the speed and then test the code again. They then saw that the Sphero had traced the same L shape but on a larger scale.
They concluded that they needed to change some-thing in the code other than the speed. Alex took the tablet and stared at the wall, as if trying to picture a pentagon. He then changed the angles in the code. They tested the code again, with the new angles, and found that the Sphero was making a different shape and kept running into walls.
They decided to test their code in a bigger space (the hallway), and Alex changed the angles again. This time, he drew the shape of a pentagon in the air with his right index finger, moving the angles on the code with his left hand as he came to each point of the shape he was drawing with his right hand. He then turned to Hakim excitedly and shouted, “I fixed the program!”
By the end of this class, Alex and Hakim had successfully adjusted the angles in their code so that the Sphero almost made the shape they wanted; however, the lengths of the sides in the code were off, so the Sphero did not yet make a closed shape.
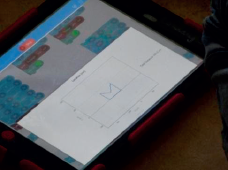
During the next class, Hakim worked to ensure that the angles in the code would make a pentagon and that he had the right number of seconds coded so that the Sphero would return to where it had started, making a closed shape. To do this, he drew the pentagon he wanted on a small whiteboard, as pictured in Figure 5. He drew lines as markers along the edges of the shape to estimate how far the Sphero should be moving along each side. He eventually got the code to a point where, as he said, “it [the Sphero] came back,” making a closed pentagon shape, as pictured in Figure 6.
Through Alex and Hakim’s creation of the code that made the Sphero move in a closed pentagon shape, we can see the thought process of computational thinking that they engaged in while getting to the shape they wanted. They started by creating a code with the right number of blocks but estimations for the angles, speeds and time, to see what the Sphero would do. As they became more fluent in the programming language, and as they came to understand how the code translated to the Sphero’s movement, they were able to make more-accurate adjustments to the code to make the shape look more and more like a pentagon. After they had created a shape with more-reasonable angles, they used a visual tool—the grid on a whiteboard—to measure how far they wanted the Sphero to roll along each side. These acts of map-ping out the shape and estimating the numbers for the code based on a drawing show that they were able to use their learned knowledge of shapes and programming to help them get the pentagon they wanted.

Painting with Polygons (Scaling)
In the next phase of the project, the teacher explained to the students how they would be using the codes they had created to paint their shapes with the Sphero. To do this, they would need to adjust their programs so that the shapes would be small enough to fit in the cardboard Sphero Arena (Figure 7).

The teacher talked to the students about the ways they could test their shapes to see if they would fit in the arena and gave them the option of estimating whether the shapes would fit. Through an open discussion on how they could scale their shapes, the students verbally showed that they understood the relationship between the code and how the Sphero would move. For example, one student suggested, “You could change how many seconds it goes for.” This student and others demonstrated that they grasped how changing the time and the speed in the code would translate to the size of their shape, showing that they were figuring out how the mathematics and the technology worked together.
As they started to use the Sphero as a paintbrush, Alex and Hakim made sure that their pentagon would fit inside the Sphero Arena by estimating its size. They then went to the arena to test their program and paint their first shape. After testing the code, they found that their pentagon fit “perfectly on the paper,” which they were ecstatic about.
With that, Alex painted a pentagon on his paper, and the Sphero moved around as expected to form a pentagon. It fit almost perfectly. During Hakim’s at-tempt, the Sphero got stuck and was not positioned the way he wanted, as pictured in Figure 8. He was upset that his pentagon did not look the way he wanted. The teacher pointed out that even though it was not quite as they had pictured it, it was still a pentagon. She said, “Do you think that making a five-sided shape deserves a high-five?” Once the teacher had acknowledged Hakim for accomplishing such a difficult task, he was satisfied with and proud of what he had created.

By the last class, the students had all painted one shape on paper, using their codes. The teacher then encouraged them to paint a second shape so that it overlapped the first shape. She talked to them about thinking “like an artist” as they thought about how they could overlap their shapes, and she explained that artists overlap shapes in various ways and that often artists have shapes at different angles crossing each other. The teacher then explained that before they painted the second shape, the students would need to determine whether it would fit in the Sphero Arena by “eyeballing” (or estimating) it.
When the students went to work on their second shape, Alex and Hakim fixed one of their previously coded rectangles to make sure that it was a closed rectangle that would fit in the Sphero Arena. When they brought the Sphero over to the arena for testing, the teacher noticed that the angles were out of order and went over it with Hakim. She helped him see that the code made an L shape instead of a rectangle and then helped him reorder the code. When they tested the program and found that the rectangle fit, Alex got excited: “It’s perfect! We can go in any rotation!” He explained that because of the size of their rectangle, they could put it anywhere on the paper, in any direction, and it would fit over the pentagon.
Alex and Hakim finished creating their artwork, and they put the rectangle in different spots over the pentagon, so that their paintings would be different, as pictured in Figures 9 and 10.


By the end of this project, both Alex and Hakim showed an understanding of how the program worked and an ability to alter their code in order to fix errors in it until it ran the way they wanted. They also showed that they had developed emotional connections with the project. This was evident in their disappointment when the artwork did not look the way they had imagined it, as well as in their excitement and happiness after it finally came together and they could see the finished product.
Conclusion
If we were to ask Grade 1 students what a pentagon looks like, not many would picture what Alex and Hakim coded as a pentagon. The students in this STEM class started seeing more (Farris and Sengupta 2016) in geometry as they traced the movements of the Sphero robots they had coded. Coding was not the end in itself in this STEM class but, rather, a secondary skill taught as a means to explore geometry more deeply.
As it was the end of the school year, the teacher designed a project in which students could paint a take-home piece by arranging polygons of their choice. The students’ pieces were all different and uniquely reflected their ownership, as seen in the case of Alex and Hakim.
Sphero robots were used in this lesson, but we are not necessarily advocating the use of Sphero (or any other commercial product that may perpetuate the instrumental agenda of STEM education). Nor are we implying that STEM class is defined by the use of technology itself. Instead, what we have shown here is how one technology can serve multiple pur-poses when the teacher’s pedagogical hopes are clear.
To create this STEM class, the teacher removed siloed desks in the classroom to facilitate collabora-tion and to create an open space where students could move their bodies freely. The teacher brought in re-cyclable materials from home for students to trans-form through their designs. In this classroom, by tracing the movements of Sphero robots in the Car-tesian coordinate system, students started to see the relationship between code and the elements of a polygon (angles and sides). As they painted with the Sphero, they encountered the notion of scale. In this pedagogical space, we demonstrated how students’ mathematical conceptualization became genetic, which Piaget (1970, 2) characterizes as “continual construction and reorganization.”
This early STEM class allowed the curriculum to be connected vertically, as well as horizontally. In terms of Alberta’s mathematics curriculum (Alberta Education 2007), the lesson described here addressed key curricular expectations for each grade level—for example, “replicate composite 2-D shapes” (p 15) for Grade 1 and “describe, compare and construct 2-D shapes” for Grade 2 (p 18). However, the lesson could be adapted to stretch students’ learning to deeper concepts—for example, “identifying examples of angles,” “classifying angles” and “demonstrat[ing] the sum of interior angles” in geometric shapes (p 37) for Grade 6. This project could also be connected to Alberta’s art curriculum (Alberta Education 1985)—for example, “shapes” and “movement of figures and objects” (p 5). In this sense, what we have documented in this article shows an expanded possibility for student learning in early STEM curriculum and pedagogy.
In these times, as we work collectively through the COVID-19 global pandemic, projects like this increasingly show their importance in early childhood education. In the midst of the pandemic, many educators are experiencing heightened difficulty in helping their young students understand abstract concepts, such as constructing and scaling shapes, with limited access to tangible learning tools that students can manipulate. Documenting pre-pandemic pedagogical innovation by teachers in public schools is, thus, important as we envision and reimagine post-pandemic education.
We asked the students, “What does STEM education mean to you?” Alex responded, “We can be scientists, and we can be anything!” As more crises arise in our world and our lives become more dependent on mathematical understanding (with and with-out technology), it is essential for young learners to see themselves in roles that will help advance the world they will live in.
Notes
- See, for example, STEM Education by Design: Opening Horizons of Possibility (Davis, Francis and Friesen 2019), which was published in alignment with the teacher education course offered at the University of Calgary.
- The names of the students have been changed to protect their anonymity.
Nicole Langevin is an undergraduate student in mathematics and education at the University of Calgary. She hopes to continue working to make STEM a more inclusive learning space for students, as both a researcher and a future teacher.
Miwa A Takeuchi, PhD, is an associate professor of learning sciences at the Werklund School of Education, University of Calgary. Through her research projects, she aims to promote equity and diversity in mathematics and STEM education.
Jenny Yuen is a beginning elementary teacher in Calgary. Prior to teaching, she completed a degree in biology. Her teaching philosophy is to make education accessible to all children. She hopes to share her passion for learning with all who cross her path.
Shayla Jaques is the mathematics and STEM learning leader at an inner-city elementary school in the Cal-gary Board of Education. She teaches STEM to students in Grades 1–6.
References
Alberta Education. 1985. Art (Elementary). Edmonton, Alta: Alberta Education. Also available at https://education.alberta.ca/media/482114/elemart.pdf (accessed October 20, 2021).
———. 2007. Mathematics Kindergarten to Grade 9. Edmonton, Alta: Alberta Education. Also available at https://education.alberta.ca/media/3115252/2016_k_to_9_math_pos.pdf (accessed October 20, 2021).
Davis, B, K Francis and S Friesen. 2019. STEM Education by Design: Opening Horizons of Possibility. New York: Routledge.
Farris, A V, and P Sengupta. 2016. “Democratizing Children’s Computation: Learning Computational Science as Aesthetic Experience.” Educational Theory 66, no 1–2: 279–96. Piaget, J. 1970. Genetic Epistemology. Trans E Duckworth. New York: Norton.
Sengupta, P, M-C Shanahan and B Kim, eds. 2019. Critical, Transdisciplinary and Embodied Approaches in STEM Education. New York: Springer.
Takeuchi, M A, and S Dadkhahfard. 2019. “Rethinking Bodies of Learners Through STEM Education.” In Critical, Transdisciplinary and Embodied Approaches in STEM Education, ed P Sengupta, M-C Shanahan and B Kim, 199–216. New York: Springer.
Takeuchi, M A, P Sengupta, M-C Shanahan, J D Adams and M Hachem. 2020. “Transdisciplinarity in STEM Education: A Critical Review.” Studies in Science Education 56, no 2: 213–53.






