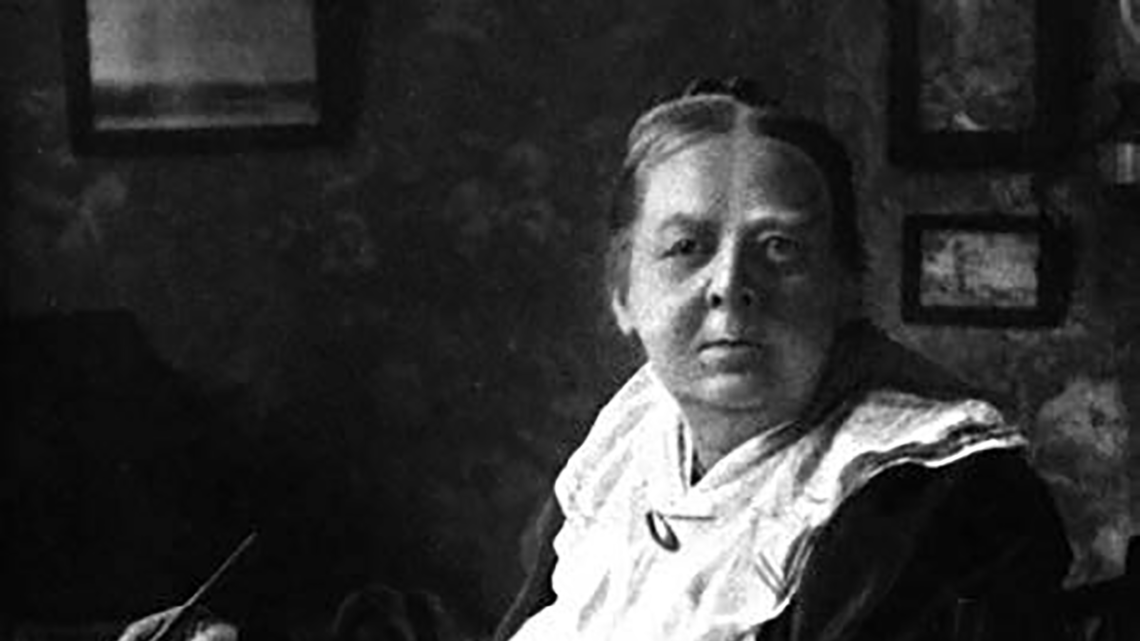Kaitlyn Neal
Mary Everest Boole. (Source: www.agnesscott.edu/lriddle/women/boole.htm.)
You may some day become a teacher. If ever you are teaching a class how to set down a sum or an equation, say “This is my way,” or “This is the way which I think you will find most convenient.”
Mary Everest Boole, Philosophy and Fun of Algebra (1909)
Mary Everest Boole was born in 1832 in Wickwar, Gloucestershire, England. During her childhood, the family moved to Poissy, France, and upon their return to England, when she was 11, she was removed from school to be an assistant to her father, who was a minister (Frost 1995).
From a young age, Boole was intrigued by mathematics. Later, she met a famous mathematician, George Boole, whom she would marry after her father’s passing (Frost 1995).
You may be wondering about the famous name Everest. Boole’s uncle, George Everest, was the surveyor general of India. He surveyed the yet-to-be-named Mount Everest and calculated its summit height; hence, the mountain was named in his honour (Frost 1995).
The first step in Boole’s career was her role as a librarian at Queen’s College, which was England’s first women’s college. Soon after, she began to teach children and was recognized as an outstanding teacher by the head of the London Board of Education. How-ever, she was forced to resign after a controversy over one of her books (Frost 1995).
Boole spent the remainder of her career and life regularly publishing books and articles (Frost 1995). In my research, I found mention of at least 21 publications authored by her. This seems to be one of her most significant accomplishments, as she left a paper trail for subsequent mathematicians and psychologists to study and review her work.
The University of Cambridge’s Darwin Correspondence Project notes that Boole “was the author of several progressive educational texts, publishing ‘The Preparation of the Child for Science’ in 1904 and ‘Philosophy and Fun of Algebra’ in 1909.”1 Those are the two books most relevant to this article.
The Preparation of the Child for Science (Boole 1904) is said to have had “a great impact on progressive schools in England and the United States in the first part of the twentieth century” (Frost 1995). Most of us are familiar with progressive teaching methods, such as cooperative learning, making content relevant, practical uses and hands-on learning. However, I was amazed to learn that a female mathematician had been practising these progressive teaching methods that long ago. Although we most often learn about these methods through the teachings of John Dewey, Boole’s ideas for progressive teaching are still very present in classrooms today.
The book I will discuss in detail is Philosophy and Fun of Algebra (Boole 1909). This book introduces readers to algebra, including word problems; solving for x, y and z; quadratic equations; square roots; and infinity. All these topics are covered throughout math education today, indicating that Boole’s ideas are still very much relevant. Throughout the book’s chapters, she explains her reasoning and logic in a uniquely creative manner.
Chapter 1, titled “From Arithmetic to Algebra,” explains how “arithmetic means dealing logically with facts which we know.” Boole emphasizes the idea of dealing logically with the known information through a word problem that involves how much a certain amount of sugar will cost. She later writes that, instead of guessing what to call a number that we don’t know, “Let us agree to call it x, and let us always remember that x stands for the Unknown.” In this chapter, we see that the mathematical language Boole used is the same language used today.
Chapter 2, “The Making of Algebras,” includes an explanation of how we approach problems. Boole states that “we make an Algebra whenever we arrange facts that we know round a centre which is a statement of what it is that we want to know and do not know.”
Boole provides examples of solving problems concurrently in chapter 3, “Simultaneous Problems.” For example,
x equals half of y;
y equals twice x;
z equals x multiplied by y.
In this problem, one cannot determine the value of x or y or z, because they depend on one another. Boole provides an algebraic way of solving the question by working through the possible answers. She argues that investing the time into this process “adds to our knowledge of the structure of Algebra, and assists us in solving other problems.”
Boole dives into quadratic equations in chapter 15, “The Square Root of Minus One,” where she refers to the square root of minus one as “an entity (or non-entity)” that “come[s] to tell us where we are to go next; and the shortest road to get there; and where we ought not to go just at present.” She suggests that the only way to solve this problem of the square root of minus one is to “treat him logically, exactly as if he were six or nine.”
In chapters 16 and 17, Boole focuses on infinity, offering problems such as the following to illustrate the concept: “Suppose there is a cake on the table. How many children can go through the room without the cake being all eaten up?”
In chapter 9, Boole describes how she uses sewing cards to help students make connections to geometry—learning the relation between dimensions. By her own account, she was very young when she connected sewing cards to curve stitching (Boole 1904; Innes 2004, 37). In modern mathematics, curve stitching is defined as “the practice of constructing straight-line envelopes by stitching colored thread through a pattern of holes pricked in cardboard” (Ross 2015). This method was devised “to help children grasp
geometric shapes, forms and structure.”2 This activity, which Boole recommended for children in kindergarten, “excites mathematical and artistic imagination but requires only the most basic skill level” (Innes 2004, 38). In classrooms today, curve stitching is mostly seen in the form of string art.
In addition to being a female mathematician and a teacher, Boole “considered herself a mathematical psychologist” (Frost 1995). She “had a lifelong interest in the unconscious mind, the psychology of learning, and how these relate to the teaching of mathematics and science” (Innes 2004, 36). She based her advice about educating children “on theories about the role of the unconscious and the psychology of learning gleaned from her own experience” (p 37).
Today, Boole is most known for her progressive teaching ideas and practices, as well as her creative methods and exercises for teaching mathematics to young children. The mathematical topics she explored in her books and her invention of curve stitching are still taught and relevant in mathematical settings today.
Notes
- “Mary Everest Boole,” Darwin Correspondence Project, University of Cambridge, www.darwinproject.ac.uk/mary-everestboole (accessed October 20, 2021).
- “Mary Everest Boole,” Darwin Correspondence Project.
Born and raised in the small town of Okotoks, Alberta, Kaitlyn Neal recently graduated with a BEd from Mount Royal University, with minors in teaching English as a second language (ESL) and mathematics. She now re-sides and teaches in Kelowna, British Columbia. After hearing a young girl say that she was not good at math because she was a girl, Kaitlyn was inspired to research and shed light on female mathematicians.
References
Boole, M E. 1904. The Preparation of the Child for Science. London: Clarendon Press.
———. 1909. Philosophy and Fun of Algebra. London: Daniel. Also available at https://etc.usf.edu/lit2go/95/philosophy-and-fun-of-algebra/ (accessed October 20, 2021).
Frost, M. 1995. “Mary Everest Boole.” Biographies of Women Mathematicians (Agnes Scott College). www.agnesscott.edu/lriddle/women/boole.htm (accessed October 20, 2021).
Innes, S. 2004. “Mary Boole and Curve Stitching: A Look into Heaven.” Endeavour 28, no 1 (March): 36–38.
Ross, G. 2015. “Curve Stitching.” Futility Closet blog, January 13. www.futilitycloset.com/2015/01/13/curve-stitching/ (accessed October 20, 2021).