Lauren D Goegan, Amy Domenique Gadsden, Wyatt Schiefelbein and Lia M Daniels
Most people have heard the term dyslexia. Popular culture often suggests that dyslexia involves the reversal of letters in words, leading to jokes such as “Dyslexics of the world, untie” or jokes about children writing letters to Satan instead of Santa. Others see dyslexia as a difficulty with understanding the sounds in words (phonological knowledge of the language). These perspectives lead people to interpret dyslexia as having an impact on young students when it comes to language (more specifically, English language arts class) but perhaps not mathematics. Indeed, dyslexia is predominantly characterized as a reading-based learning disorder that can also affect writing. Challenges in mathematics are often labelled as math-based learning disorders (such as dyscalculia), which is a separate category.
Although dyslexia is often diagnosed and treated as separate from mathematical skills, one can be diagnosed with both dyslexia and dyscalculia. More-over, difficulties in reading and math can have similar underlying challenges, including effects on working memory, processing speed and oral language comprehension (Willcutt et al 2013). The experiences in math class of students with dyslexia can provide in-sight into how dyslexia affects learning and performance in mathematics and how teachers can support these students.
Toward that end, this narrative article has two main sections. First, we present the retrospective first-person stories of three students with dyslexia, who offer various viewpoints on what it is like to be a student with dyslexia in an elementary math class. Second, through these stories, we explore the op-portunity to identify and adapt practices in the classroom.
These accounts are meant to help teachers think about their own teaching practices and how best to support student diversity in the classroom, building on the idea of universal design for learning (UDL) and motivation design principles. This examination is both timely and important. As the Alberta Educa-tion website states,
Future curriculum focuses on foundational elements, such as reading, writing, and arith-metic, while also incorporating competencies like problem solving and critical thinking.
Literacy and numeracy foundational ele-ments are in every subject and at every grade level, and with greater emphasis on the devel-opment of competencies.1
Therefore, supporting students with dyslexia when it comes to mathematics instruction is vital.
Stories of Three Students with Dyslexia
Story 1: Misreading the Problems
I always hated math class. However, as I look back on my time in elementary school, I wonder if this hatred stemmed from the math itself or from the words associated with math.
The first time I remember disliking math was in Grade 2. As part of math class, we learned how to spell all the numbers up to 100. For a student who couldn’t spell in general, having to spell in math class was terrible. To make matters worse, the paper would always come back covered in red ink from all my spelling mistakes, undoing any positive attitude I may have had toward math. Those days, it felt like math class was just an extension of English language arts, and all I wanted was more numbers and fewer words. Then, once we had learned how to spell all the num-bers, we were given math tests that contained no numerals, only spelled-out numbers. I was lost in the sea of words, and I felt like I was drowning. I couldn’t read questions properly, making it impossible for me to ever really get to the “math part” of a question. I often sat in class frustrated, knowing that I could do the math but unable to see the math in front of me. The teacher seemed to ignore my challenges and just told me to try harder next time.
Things didn’t get any easier in the years to come, as math worksheets and tests began to include word problems. To this day, I refer to word problems as a reading test. The first time I remember encountering word problems was in math class in Grade 4. We were completing a unit on medieval times, and the word problems reflected this theme. Therefore, on top of the usual words I couldn’t read, this unit introduced a new, specific vocabulary, which I also could not read. The words prevented me from showing what I actually knew in math because I had no idea what the questions were asking. My strategy was to guess what math skills the words were trying to get at: a big number with a small number probably meant a sub-traction question; two bigger numbers probably meant addition. Guessing is never very accurate, and the red ink once again covered my paper. The words continued to get in the way, even though I could answer all the questions when they used numerals.
After a few tests like this, my teacher began to real-ize that something was going on when it came to the word problems. This teacher took the time to look at my tests and recognized the pattern in my errors. She recognized that my mistakes could be attributed to the words and not the math, and she was willing to make changes to support my success.
Specifically, she began to read the math tests aloud to me. Something about this combination of auditory and visual information supported my comprehension of the questions. Once I could understand what a question was asking, I could perform the necessary mathematical operation, and the red ink began to disappear. This supported my learning and became a strategy for solving word problems in the future. Of-fering multiple modalities for students can support the various learning needs in the classroom.
Story 2: Misunderstandings and Misperceptions
As an elementary student with dyslexia and other learning disabilities, I had many deeply wounding experiences, especially in math. As early as kinder-garten, the impact of my disabilities was visible to others, as well as to myself. I had difficulty with expressive language, including articulation of letters and numbers, which included reversal, inversion and overall production. At the time, this was attributed to a behavioural challenge rather than a developmental one. As a consequence, I was often “othered” by peers and teachers. I felt the impact of my disabilities in how others responded to me, which affected my self-esteem, self-efficacy and self-worth.
One of my most devastating math experiences oc-curred in Grade 4. I had experienced much under-achievement and failure in math up to then. I often felt frustrated in math class because of the amount of time I needed to attend to the lesson, write down the instructions and notes, process the instructions and notes, apply new knowledge, and ask questions and problem solve. As a consequence, I would often disengage and cry. I felt humiliated and stupid.
The specific incident took place following a sum-mative assessment on long division. The teacher walked around the classroom, returning our tests. The silence as she passed my desk was deafening. She offered praise or encouragement to other students, but she had no words for me. Her silence felt like a punishment, a reinforcement of my inadequacy and inability. I felt shame. I turned my paper over. Red ink everywhere. Circles and lines scarred my worth-less work. Every answer was wrong. On the bus ride home, I cried so much that the red turned to pink, and all that remained of my work were faint pencil lines.
My turning point in mathematics happened a few years later. After continued failure and underachieve-ment, I was incredibly anxious about an upcoming test on fractions. I couldn’t keep up in class—every-thing was moving too fast. Thankfully, an empathetic, patient and skilled substitute teacher changed the course of my achievement in math forever.
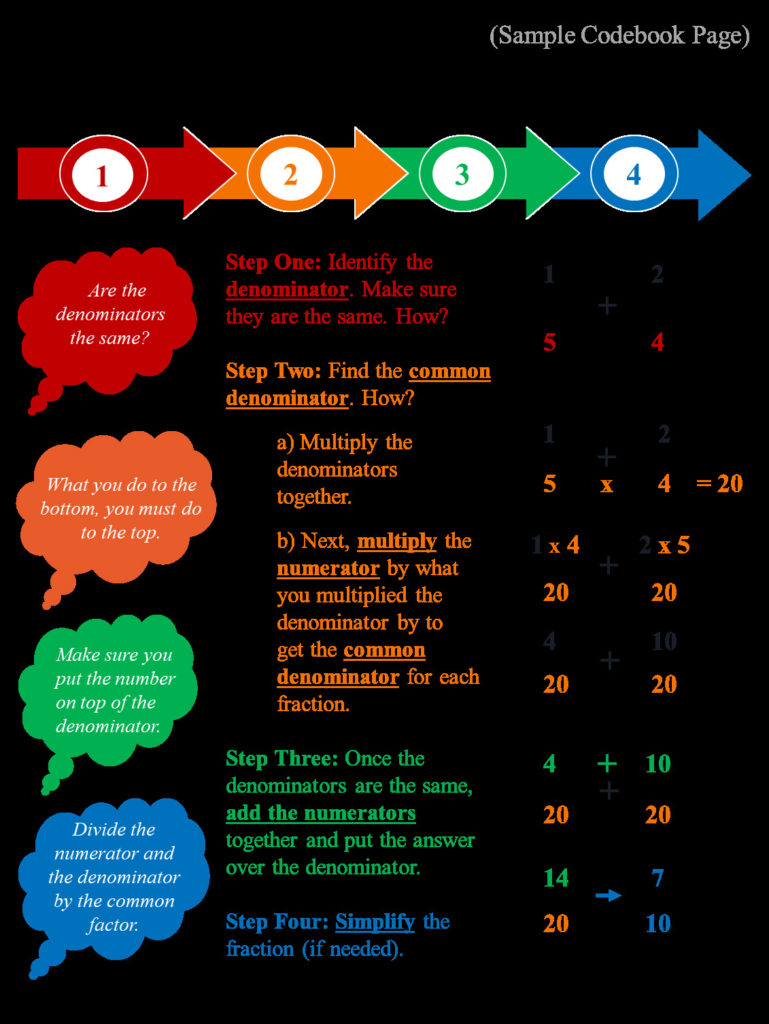
She sat with me for an entire morning, teaching me the fundamentals of fractions and the order of operations involved in solving problems. She helped me identify my challenges and areas of need, and asked me insightful questions that forced me to con-struct my own strategies to mitigate the impact of my disabilities in math. She took the time to respond to my questions, soothed my anxiety and was sensitive to my frustration. She also helped me construct a code book of sorts that outlined the steps involved in solving problems in multiple modalities (diagram, text, orally) that made sense to me—a key reference that would enable me to study outside of class to reinforce concepts (see Figure 1). Following this, I was motivated and committed to showing both myself and my teacher that I could be successful, that I was capable and that I did understand. The result was my first A ever in math!
That teacher helped me develop academic self-efficacy, which improved my self-esteem. As a result, I was more willing to take risks, advocate for myself and accept the impact of my disabilities as specific rather than global.
Story 3: Miscommunication When Asking Questions
In math class, I had a lot of trouble. Certain expectations in math were perhaps a bit beyond what I was capable of at the time—for example, times tables. I still don’t know my sixes, sevens and eights, and I am not keen to learn them now. My experiences with word problems in math were less than ideal. I struggled with decoding the words, especially in terms of what aspects of the question were relevant. The lack of empathetic support led me to believe that my teach-ers were eager to fail me. They did not seem eager to support my learning needs in their classrooms.
Aside from all this, a major factor contributing to my poor performance in math class was miscom-munication. I felt like my teachers couldn’t under-stand me and the questions I asked. Oral language difficulties, such as problems conveying my ideas, often hindered my performance in math class, especially when I was required to explain my work. While I enjoyed math, math class itself was often a trying time for me.
I imagine that most people have had an experience like this: you say something you think is intelligible and receive in return a blank stare or, worse, a hesitant answer to a question you did not ask. In elementary school math class, this happened to me regularly, and it was the height of embarrassment.
Sometimes I would press on, trying to find a new way to phrase my question. After all, maybe my wording was the problem. This strategy worked maybe twice, and when it did, I felt like the teacher appreciated what I was bringing to the classroom and recognized that I was capable of understanding the material at hand. When it didn’t work—which was most of the time—I was mortified, because now my peers were frustrated with my persistence and appar-ent lack of understanding.
I learned that it was easier to pretend the teacher had answered my question. I spent a lot of time in elementary and middle school pretending I had asked questions I had not asked. This saved me some embar-rassment, but I felt largely on my own when it came to learning math. Often, it felt like teachers assumed what I was going to ask, and that was the question they would then answer, regardless of what I had actu-ally intended. Challenges with oral language com-munication had an impact on my math performance, as I did not feel that I was on the same page with my teachers.
But to say that I was bad at math would be a mis-take. I was rather good at math. I understood how math could be helpful in many contexts and, thus, why it was important to learn.
As I struggled to communicate in math class, I turned to a different place to learn math: art class. Through art, I could explore math in all kinds of ways. Multiplication, division, fractions, algebra, geome-try—everything mathematical related to art in really fun and interesting ways. And the art teachers had fewer expectations as to what kinds of questions I would ask—miscommunication rarely happened dur-ing art class for me. My words worked there, even to sort out math. Because of this, I sincerely believe I learned more math in art class than I did in math class. Art allowed for visual exploration of concepts and ideas, an area of self-expression at which I felt adept. Art provided the freedom to explore how math was important to my goals. What is more, I was good at art, and thus I needed to be good at math. So I developed my math skills as they related to art.
The lesson in this story is that, as educators, we must try to really understand what a student is asking. Miscommunication is quite natural, but it takes two people to recognize that it is happening in order to then address it. Based on my own experiences with dyslexia, I would say that the root of the diagnosis is miscommunication—in my case, miscommunication that was exacerbated in math class but mitigated in art class.
Learning from These Misadventures
The stories of these three students highlight how students do not leave their dyslexia at the door of the math classroom. Dyslexia has major implications for math learning, performance and motivation. From these stories, we can extract important considerations for a responsive and inclusive math classroom that would align with Alberta’s vision and advocacy for an inclusive education system.2
Universal Design for Learning
Universal design for learning (UDL) allows for the development of flexible learning environments that can accommodate individual learning (Edmunds and Edmunds 2018). The challenges described by the three students with dyslexia could have been miti-gated with the application of UDL to math class.
The Center for Applied Special Technology (CAST) outlines three UDL guidelines: multiple means of representation, multiple means of action and expression, and multiple means of engagement.3 Next, we describe how these guidelines could have improved the experiences of the three students.
Multiple Means of Representation
The first UDL guideline recommends providing students with multiple means of representation.
The first and second stories highlight how having access to multiple means of representation is vital for learners with disabilities. It gives them different ways to communicate and access information. For example, both stories underscore how providing alternatives to written information can contribute to better under-standing. In the second story, offering ways to customize the display of information could have sup-ported the student’s understanding of the mathematical concepts to be learned.
As evidenced in all three stories, not all students learn best from reading, particularly those who have difficulty with breaking down the sounds in words, or those who have below-grade-level reading abilities. Furthermore, clarifying new vocabulary or words needed to complete the task can help reduce students’ challenges with comprehension of word problems. Students must have equitable access to the content of questions so that they can meaningfully contribute to in-class activities in a timely manner. That is, time should be spent on comprehension and the develop-ment of requisite skills (such as problem solving) rather than on decoding. Knowing the words in a question is central to being able to answer that question.
Also, highlighting critical features and big ideas in a lesson can be instrumental in supporting those who have challenges with working memory or processing speed. A big idea is a place where all students can start, and they can build their knowledge from there. Using big ideas is particularly helpful for those with dyslexia because it gives them structure on which to build their learning.
Multiple Means of Action and Expression
The second guideline for UDL is multiple means of action and expression. Action and expression refer to the how of learning.
Indeed, in the second story, the teacher probed the student’s learning by using questioning to help the student develop strategies for future challenges in math. This can serve as a think-aloud approach to better understand the gaps in a student’s learning and how the student is making sense of the content. This approach allows the teacher to understand where the student is and to build from there, and it allows the student to be active in the learning process.
Furthermore, developing a code book with a check-list or template gives students an excellent reference for when they encounter similar problems in the fu-ture. This allows them to manage information and resources in a format that is accessible and that sup-ports their learning needs. All students can develop a code book related to how they learn best. One student might write out the concepts, one might draw, and one might use different colours. Students can use a format consistent with how they learn.
This guideline could also be a consideration for word problems. Is there another way that word prob-lems can be presented to show learning of math concepts? Indeed, in the first story, using a medieval setting for word problems required that students understood more concepts and terms than just those presented in math. This situation can be particularly challenging for students with dyslexia, who may struggle with vocabulary as a result of below-grade-level reading skills. While teaching across curricula can have benefits, using real-life scenarios in word problems might be more helpful for students who struggle with words. Building from that, acting out a word problem to ensure that students understand the content before they attempt to answer the math com-ponent can assist students with dyslexia.
Multiple Means of Engagement
The third guideline for UDL—and an important component of learning—is multiple means of engagement.
All three stories describe students who sat in class disengaged, uninspired, frustrated or even in tears. A teacher’s use of a red pen was mentioned in two of the stories as a practice that the students experienced as punitive and unsupportive of their learning, as well as one that undermined their sense of self-efficacy and self-worth. Teachers must ensure that the learning environment is supportive and that it is a place where mistakes can happen and are, in fact, encouraged.
Teachers can support student engagement by creat-ing opportunities for cooperation and collaboration in class and by facilitating a community environment. For example, in the first story, the student who struggled with the reading aspects of the word prob-lem could have been paired with a student who had challenges with the numbers. Using their strengths to offset their challenges and to support each other can help students see that everyone has both strengths and areas of need. Furthermore, this can allow for meaningful peer interaction and the development of friendships, which is particularly important for those with learning disabilities, as they often have difficul-ties with social skills (Wiener and Schneider 2002).
Additionally, when it comes to engagement, help-ing students develop personal coping skills and strate-gies is imperative. As seen in the second story, stu-dents who have challenges in the classroom can experience high levels of anxiety and frustration. Having resources to manage that frustration and to develop coping strategies when challenges arise is important for students’ engagement, achievement and continued motivation. In the third story, miscommu-nication was discussed as presenting obstacles to the learner in math class, but it was not an issue in art class. Math teachers must be as willing as teachers in other subjects to be patient, to understand the learner and to engage in meaningful dialogue.
Motivation Matters Most
In a video about UDL, David Rose, cofounder of CAST, notes that engagement is perhaps the most important component of UDL: “If we don’t engage students in learning, don’t make it important to them, make them motivated for it, then none of the other forms of representation or expression will be that important” (National Center on Universal Design for Learning at CAST 2010, 4:30). Therefore, we want to highlight the importance of supporting student motivation in the classroom.
Researchers at the Alberta Consortium for Motiva-tion and Emotion (ACME), a research group that supports graduate students from programs across the Department of Educational Psychology at the Uni-versity of Alberta, have been examining motivation design principles (Linnenbrink-Garcia, Patall and Pekrun 2016; Radil 2017). The five principles are as follows:
• Supporting student competence
• Enhancing autonomy
• Designing personally relevant and active tasks
• Modelling learning
• Encouraging relatedness
Next, we discuss how these five principles are relevant to students with dyslexia in math classes.
Supporting Student Competence
The first motivation design principle involves sup-porting student competence through well-designed instruction or encouraging feedback (Linnenbrink-Garcia, Patall and Pekrun 2016).
The three stories from students with dyslexia de-scribe how hard it is to maintain motivation in math class when the words in word problems prevent students from accessing the numbers; when their ef-forts are met with red ink, large Xs and silence from teachers; and when their questions go unanswered. In contrast, well-designed instruction that embraces multiple modalities of presenting information or that provides multiple avenues for working with the in-formation helps students learn and apply new knowledge and skills. When teachers ensure that students can get through the words to reach the math and then experience success, students’ motivation increases.
Enhancing Autonomy
The second motivation design principle is autono-my. This involves allowing students to make decisions about or exercise control over aspects of their learning (Linnenbrink-Garcia, Patall and Pekrun 2016).
The students in the three stories experienced almost no control over their own learning; rather, they pas-sively tried to meet the requirements set out by their teachers. However, the example of creating a code book that the student could access outside the class-room shows how empowering students not only sustains their motivation but can also bring about success.
Designing Personally Relevant and Active Tasks
The third motivation design principle is task de-sign, which involves selecting relevant and interesting activities in order to facilitate active involvement (Linnenbrink-Garcia, Patall and Pekrun 2016).
Again, the three stories of students with dyslexia do not mention class activities or assignments linked to the students’ interests. Rather, the stories describe the students’ challenges with the tasks teachers pre-sented to them and the challenge of completing those tasks with interest largely absent.
Student interest is an important consideration—not only with students with dyslexia but with all students in the classroom.
Modelling Learning
The fourth motivation design principle is model-ling learning, which includes demonstrating a good attitude toward students and teaching with enthusiasm and energy (Radil 2017).
The importance of this principle can be seen most clearly in the second story. The first teacher men-tioned by the student was not seen as having a positive attitude toward the student’s learning challenges, and the teacher’s silence when returning tests is a salient memory for the student decades later. However, the second teacher, who sat and worked with the student, had a positive effect on how the student thought and felt about him- or herself, transforming the student’s frustration and feelings of inferiority into a sense of possibility.
Teachers can make all the difference through their own attitudes and enacted forms of those attitudes. Positivity and possibility are contagious (Frenzel et al 2018). Teachers set the tone through their modelled and enacted attitudes and behaviours.
The value of modelling learning is also discussed in the third story. The lack of enthusiasm and energy in the math classroom, which arose from a sense of generalized miscommunication, inhibited the stu-dent’s active participation in classroom activities. Conversely, exciting and creatively engaging activi-ties in art class fostered the student’s enthusiasm for math as a means to achieve personal goals and ambi-tions, which in turn improved the student’s math skills markedly.
Encouraging Relatedness
The fifth motivation design principle is relatedness, which means that students feel supported and have a sense of belonging among other students and their teachers (Linnenbrink-Garcia, Patall and Pekrun 2016). This can include developing genuine and car-ing relationships and a sense of community, which is critical to facilitating an environment where diversity is celebrated.
This sense of community was markedly absent in the third story. The student was uncomfortable with rephrasing a question that the teacher had misunderstood the first time, and the student felt a sense of impatience and pressure to remain quiet from peers. Developing a sense of relatedness helps students feel comfortable with asking questions and making mistakes.
On the other hand, a sense of relatedness was pres-ent in the second story, in the form of the teacher’s enacted empathy and genuine investment. The student was able to articulate and identify this relatedness based on the behaviour of the teacher. Teachers who take the time to show genuine investment and caring are able and willing to develop positive relationships with students (Noddings 1991).
Starting a New Adventure
The math class misadventures experienced by the three students with dyslexia have allowed us to ex-plore UDL guidelines and motivation design princi-ples for students with diverse learning needs in the classroom. We hope that the students’ accounts gener-ate reflection and meaningful discourse about current pedagogy and teacher practice. If nothing else, these stories highlight that dyslexia is not a concern only in English language arts class. It also affects students’ ability to access math concepts, as well as their con-fidence in expressing themselves more generally.
Notes
1. See www.alberta.ca/curriculum-development.aspx (ac-cessed August 8, 2019).
2. See www.alberta.ca/inclusive-education.aspx (accessed August 8, 2019).
3. See http://udlguidelines.cast.org (accessed August 8, 2019).
References
Edmunds, A, and G Edmunds. 2018. Special Education in Canada. 3rd ed. Don Mills, Ont: Oxford University Press.
Frenzel, A C, B Becker-Kurz, R Pekrun, T Goetz and O Lüdtke. 2018. “Emotion Transmission in the Classroom Revisited: A Reciprocal Effects Model of Teacher and Student Enjoyment.” Journal of Educational Psychology 110, no 5 (July): 628–39.
Linnenbrink-Garcia, L, E A Patall and R Pekrun. 2016. “Adaptive Motivation and Emotion in Education: Research and Principles for Instructional Design.” Policy Insights from the Behavioral and Brain Sciences 3, no 2 (October): 228–36.
National Center on Universal Design for Learning at CAST. 2010. “Universal Design for Learning (UDL): Principles and Practice.” YouTube video, 6:35. March 17. www.youtube.com/watch?v=pGLTJw0GSxk (accessed August 8, 2019).
Noddings, N. 1991. The Challenge to Care in Schools: Rethinking the Goals of Education. Williamsburg, Va: College of William and Mary.
Radil, A I. 2017. “Teachers’ Perspectives on Motivational Practices in Classrooms: An Exploratory Sequential Mixed Methods Design.” PhD dissertation, University of Alberta. Also available at www.library.ualberta.ca/catalog/8197767/ (accessed August 8, 2019).
Wiener, J, and B H Schneider. 2002. “A Multisource Exploration of the Friendship Patterns of Children With and Without Learning Disabilities.” Journal of Abnormal Child Psychology 30, no 2 (April): 127–41.
Willcutt, E G, S A Petrill, S Wu, R Boada, J C DeFries, R K Olson and B F Pennington. 2013. “Comorbidity Between Reading Disability and Math Disability: Concurrent Psychopathology, Functional Impairment, and Neuropsychological Functioning.” Journal of Learning Disabilities 46, no 6 (November/December): 500–16.
Lauren D Goegan is a doctoral candidate in the Department of Educational Psychology at the University of Alberta. Her doctoral research examines the transition from high school to postsecondary education, particularly for those with learning disabilities. She also researches various stakeholder definitions of success (including those of teachers and students).
Amy Domenique Gadsden is a doctoral candidate in the Department of Educational Psychology at the University of Alberta. Her research areas include special and inclusive education, policy, and practice. Specifically, she conducts research that focuses on students with learning disabilities in higher education.
Wyatt Schiefelbein is a graduate student at the University of Alberta, pursuing a master of education degree in interdisciplinary studies with the Department of Educational Psychology and the Faculty of Native Studies. His research examines the intersections of ableism, racism, science and education through conceptions of the terms learning disability and intelligence.
Lia M Daniels is a professor in the Department of Educational Psychology at the University of Alberta. Her research examines student and teacher motivation and emotions, with the hope of creating supportive learning environments.