Richelle Marynowski and Landry Forand
The Alberta K–12 mathematics program of studies includes three sequences at the secondary level (“-1,” “-2” and “-3”), each intended as prerequisites for specific postsecondary programs or direct entry into the workforce (Alberta Education 2008). Students progressing into Grade 11 are tasked with choosing the mathematics course sequence that will best fit their future goals. Choosing between sequences can be stressful for both students and parents. Confusion exists with parents about the goals and purposes of the mathematics sequences as many of them experienced a different set of mathematics courses and, for some of them, a different structure in high school in general (Palfy, McFeetors and McGarvey 2020).
There seems to be a lack of options for students progressing to university who take the “-2” sequence.
Each sequence is designed to provide students different pathways to suit their future goals and their strengths in mathematics. The implementation of these sequences initiated in 2008 to replace the Pure and Applied Mathematics sequences, which had been in place since 2000 (Alberta Learning 2002a, 2002b). Unlike Pure and Applied Mathematics, the new sequences would not vary on difficulty, but on content. Specifically, the Mathematics “-1” and “-2” sequences would be of similar difficulty; one course would not be easier than the other, and differentiation of content would define each sequence. The “-1” and the “-2” sequences were specifically developed for progress into postsecondary mathematics, while the “-3” was for entry into the workforce or as a gateway into trades programs (Alberta Education 2008). Additionally, unlike the previous Pure and Applied Mathematics sequences, the structure of the content in the mathematics “-1” and “-2” sequences allows for students to move between sequences if their plans for postsecondary change.
The focus of this study is on the “-1” and “-2” sequences and their mapping onto first-year university courses. The intentions for the two sequences linking to postsecondary are as follows:
“-1” Course Sequence
This course sequence is designed to provide students with the mathematical understandings and critical-thinking skills identified for entry into post-secondary programs that require the study of calculus. Topics include algebra and number; measurement; relations and functions; trigonometry; and permutations, combinations and binomial theorem.
“-2” Course Sequence
This course sequence is designed to provide students with the mathematical understandings and critical-thinking skills identified for post-secondary studies in programs that do not require the study of calculus. Topics include geometry, measurement, number and logic, logical reasoning, relations and functions, statistics, and probability. (Alberta Education 2008, 57)
Both the “-1” and the “-2” sequences include a variety of specific outcomes aimed to fulfill the description above. The “-1” sequence is specifically for programs that require calculus in postsecondary, and “-2” is for studies that do not require calculus. The choice to focus on university courses and not other postsecondary options was specifically due to the nature of the change in the Alberta program of studies from 2002 to 2008 in intending “-2” to be a viable entry to university studies.
Previous research showed that the “-2” sequence is not represented as a common program prerequisite when students are transitioning to university studies (see Marynowski and Forand 2016, 2017a, 2017b, 2017c). This study was developed to delve deeper into what specific outcomes from the “-1” and “-2” program of studies were relevant to specific first-year university-level courses. Information gathered from five Alberta universities (University of Lethbridge [U of L], University of Calgary [U of C], University of Alberta [U of A], Mount Royal University [MRU] and MacEwan University [MU]) found that Mathematics 30-2 does not provide as much access to faculties, programs or courses as was potentially intended. Knowing this, even for a student who shows no interest in programs containing calculus, that student may find it logical to choose Mathematics 30-1 to maintain a higher range of options for a university career. Additionally, 40 first-year math courses from the 2016/17 academic year were identified from the same five Alberta universities where Mathematics 30-1 was identified as a prerequisite option for all 40, and Mathematics 30-2 for only 11 of those courses. Only 15 of the 40 courses were calculus based, implying that the other 25 courses could potentially accept Mathematics 30-2 as a prerequisite or require no prerequisite (Marynowski and Forand 2017b).
What specific content from the Grade 12 mathematics courses in Alberta are required for first-year mathematics courses in universities in Alberta?
Despite the intentions of Alberta Education, there seems to be a lack of options for students progressing to university who take the “-2” sequence even though the number of students taking Mathematics 30-2 is increasing. From 2014 to 2018, the average number of students who wrote the Mathematics 30-1 diploma examination was 20,670, and the average number of students who wrote the Mathematics 30-2 diploma examination was 13,385. The number of students writing the Mathematics 30-1 diploma examination has been reduced by approximately 1,200 students over that five-year period, and the number of students writing the examination for Mathematics 30-2 has increased over the same time period by approximately 2,300 students (Alberta Government 2021).
The questions that arose from the previous research, and that this study strives to answer, are What specific content from the Grade 12 mathematics courses in Alberta are required for first-year mathematics courses in universities in Alberta? and Are the current first-year university mathematics course prerequisites appropriate for the skills that students need in that course?
To respond to these questions, a study was under-taken to map the specific outcomes from the Alberta Mathematics 30-1 and 30-2 program of studies to the first-year mathematics courses at five major universities in Alberta. The study consisted of surveying mathematics faculty and instructors at the same universities (U of L, U of C, U of A, MRU and MU) that were included in the previous study on course prerequisites.
Research Process
An electronic survey was developed and sent to the mathematics faculty and instructors at the five universities. Five unique surveys were created: one for each institution. Each survey included the specific course names and numbers that were offered at that institution and were sent to each institution’s respective mathematics department faculty and instructors. Faculty and instructors from each institution were invited to select specific outcomes from the Grade 12 mathematics courses that mapped directly to a specific first-year course. Each respondent selected what first-year classes they were taught and then chose the outcomes from the “-1” and “-2” sequence that fit best as a prerequisite for their selected courses.
To avoid redundancy of outcomes being shared between Mathematics 30-1 and 30-2, the following outcome from Mathematics 30-1 was not included in the survey: “Demonstrate an understanding of logarithms” (Alberta Education 2008, 22), and the fol-lowing six outcomes from Mathematics 30-2 were removed from the survey:
- “Solve problems that involve permutations.” (p 29)
- “Solve problems that involve the fundamental counting principle.” (p 29)
- “Solve problems that involve combinations.” (p 29)
- “Solve problems that involve rational equations.” (p 30)
- “Demonstrate an understanding of logarithms and laws of logarithms.” (p 30)
- “Solve problems that involve exponential equations.” (p 30)
These outcomes are identified as falling under “both” sequences as they appear in both the “-1” and “-2” sequence. Additionally, the outcomes from the “-1” and “-2” courses were listed in no particular order and were not identified as being from a specific sequence so that there was no bias in the mathematics faculty or instructors selecting outcomes from one particular sequence or another.
The surveys also included open-response questions that invited mathematics faculty and instructors to provide comments on the following:
- Topics you would like to see added or removed from secondary mathematics courses in Alberta.
- Strengths or weaknesses of students in introductory mathematics courses taught before, during or since 2012.
- Other comments pertaining to secondary mathematics education in Alberta.
Grade 12 “-1” and “-2” mathematics curriculum in Alberta were implemented in 2012, following changes to Grade 10 in 2010 and Grade 11 in 2011.
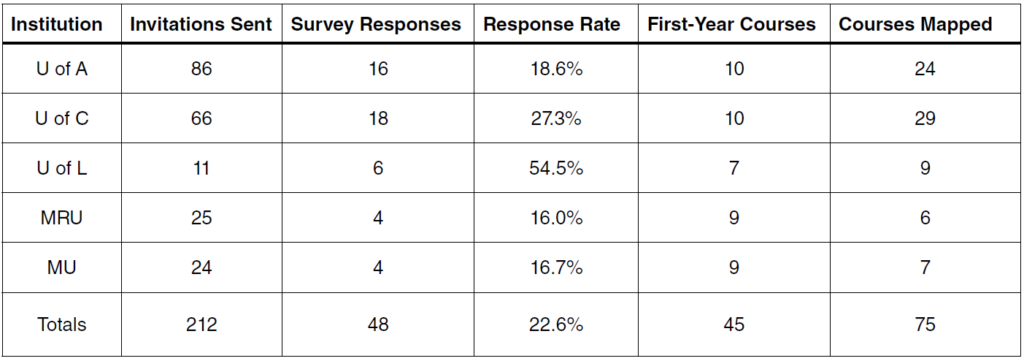
Invitations to complete the survey were sent to 212 mathematics faculty and instructors whose names and e-mail addresses were publicly available on university websites. Invitations were sent in July, and reminders were sent in mid-August. Table 1 shows the the number of invitees, respondents and courses that were mapped per institution. Not all of those invited taught first-year classes, which may partly account for the response rate.
Out of 48 respondents, 43 answered some or all of the open-response questions. Some taught more than one first-year course, so the total number of courses mapped was more than the number of respondents.
Survey Responses
Data was summarized in terms of the number of times a specific outcome was selected. Responses to open questions were analyzed using thematic analysis (Braun and Clarke 2006); themes were identified within questions, and responses across questions were analyzed for global themes. Additionally, comments that were particularly poignant or noted an alternative perspective were highlighted for comparison. The quantitative data is presented first and the qualitive data is presented second.
Outcome Frequency
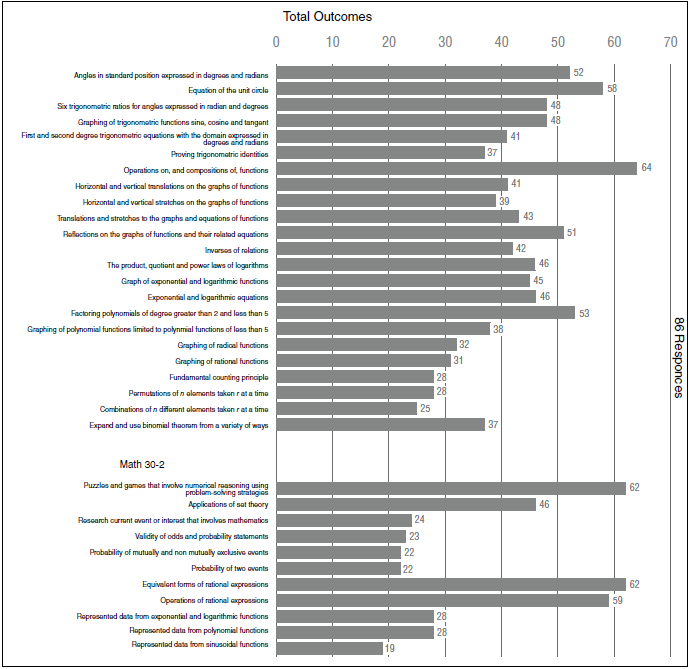
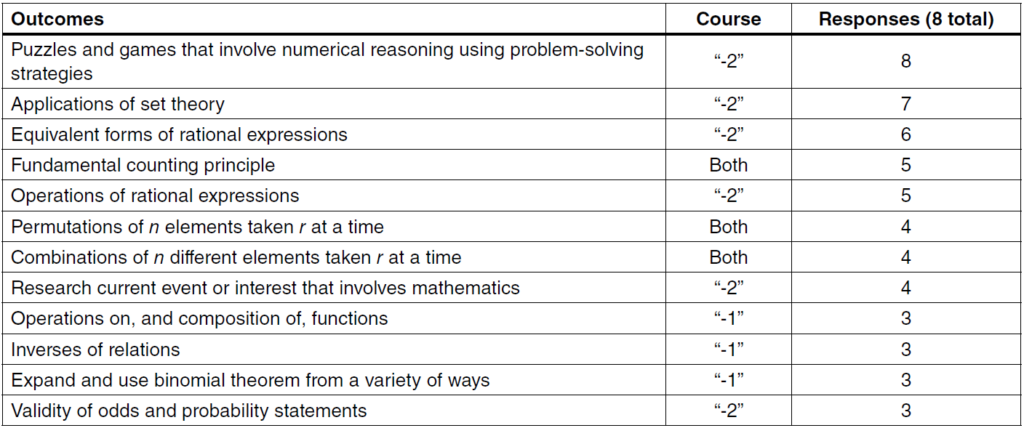
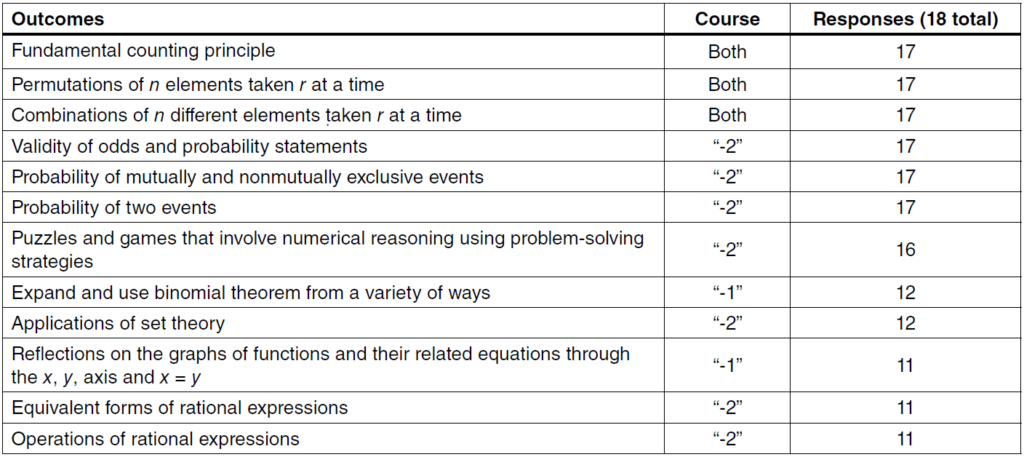
Figure 1 illustrates the number of times each out-come was selected as an appropriate prerequisite for a first-year university mathematics course.
As illustrated in Figure 1, the five outcomes that were most frequently selected as important for first-year mathematics courses were equation of the unit circle, operations on and compositions of functions, puzzles and games involving numerical reasoning, equivalent forms of rational expressions and operations on rational expressions. Three of these five are only addressed in the Grade 12 “-2” course, though rational expressions outcomes also occur in the Grade 11 “-1” course, implying that the students completing the “-1” Grade 12 course would have also been introduced to those outcomes.
courses.
For purposes of analysis, the first-year university courses were split into four categories: calculus, statistics, reasoning and linear algebra, allowing us to relate outcomes to specific course style to deter-mine if the outcomes from the “-1” or “-2” courses were mapped as intended by Alberta Education. Tables 2 through 5 illustrate the top selected outcomes for each first-year university course type.
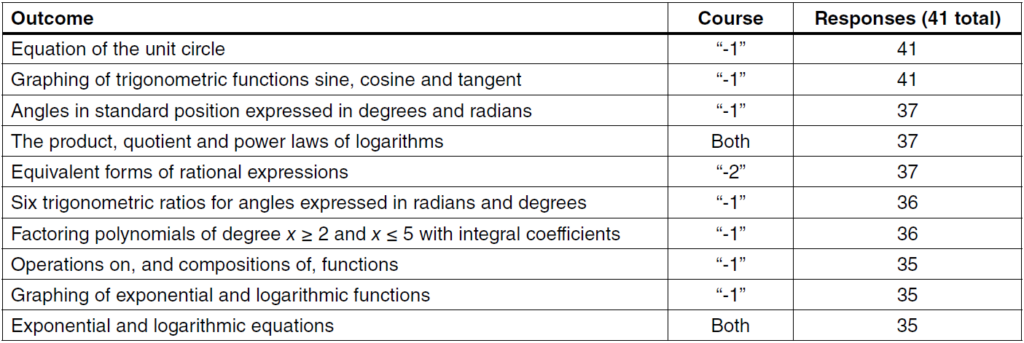
In Table 2, we can see that the outcomes from Mathematics 30-1 map strongly to first-year calculus courses. Thus, it appears that “-1” is an appropriate prerequisite for calculus.
Identified prerequisites for linear algebra (Table 3) were primarily found in Mathematics 30-1, possibly due to the abundance of trigonometric outcomes in the course. Linear algebra is not a calculus course, but currently Mathematics 30-2 does not offer necessary background. Adding additional trigonometry to the “-2” course might help it align more clearly with linear algebra.
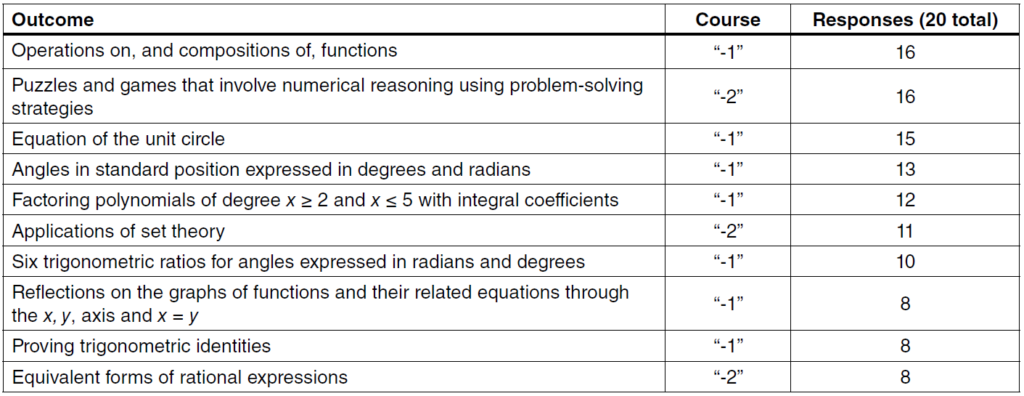
In reasoning courses (Table 4), students learn higher arithmetic, discrete math and proofs. Here, the majority of outcomes were chosen from Mathematics 30-2; the U of A and MU are the only institutions of the five that take Math 30-2 as a prerequisite for their reasoning courses.
All but 2 of the 12 top outcomes for statistics align with Mathematics 30-2, which is consistent with the intention that the “-2” sequence be a prerequisite for courses not involving calculus (Table 5). However, many statistics courses require Mathematics 30-1.
Qualitative Data
At the end of the survey we asked a series of open-ended questions about specific topics they wanted included in or removed from the secondary mathematics program, and about strengths and weaknesses of students before and after the curriculum changed. General response questions also allowed them to comment on other matters they deemed relevant. A total of 43 university faculty and instructors representing each of the five universities responded to the open-ended questions. There were eight open questions that garnered 152 comments. Comments ranged from one word to paragraph responses. Regardless of the prompt, comments centred on the following themes: specific mathematics content, specific mathematics skills, and student attitudes and behaviours. Themes are presented below along with illustrative examples of specific comments.
Specific Math Content
The prompt that received the most comments regarding specific math content was the one asking participants what topics should be included in the secondary mathematics curriculum. Of the 152 comments, 16 focused on logical reasoning and proof, noting this as either a weakness or as something that needs to be added and stressed in secondary mathematics. One respondent commented:
Logical reasoning is the main thing. Basic under-standing of propositional logics: negations of statements, the logical connectors “AND” and “OR” as well as the extremely important “IF…
THEN….” Ideally also basic exposure to statements with quantifiers. Basic use of logical deductions. Familiarity with valid arguments, and with fallacies (invalid arguments).
Even on the questions that asked for strengths of students, the comments regarding logical reasoning and proof identified this as a weakness and as an important aspect to mathematics learning overall.
Other content areas mentioned multiple times included manipulating fractions (10 mentions), geometry (7 mentions), statistics (4 mentions) and calculus (3 mentions). Being able to work fluently with and understand fractions was noted as a weakness of students in first-year university classes after 2012. One participant commented: “I think whether or not students properly learn to manipulate fractions at the junior high level (and practise it until it is second nature) plays a bigger role in determining their success in later courses than any particular curriculum choices at the high school level.” Geometry (classic plane geometry, Euclidean geometry, analytic geometry) was noted as a topic that could be more high-lighted or included in the secondary mathematics curriculum, as was statistics. One participant detailed particular requests: “How to collect data for mathematical or statistical problems. How to make inter-pretations or conclusions from calculations based on the data. Limits of the validity of the conclusions given the limits of the data.” Two responses suggested removing calculus from the secondary program; another identified limits as a common weakness.
On the positive side, one participant noted: “I think the cohorts I taught around 2010, give or take a couple of years, were the strongest I’ve had. The pre-Engineers were superbly prepared in every way for introductory Calculus.” A second participant commented that students are “generally able to handle algebra and trigonometry with a 70 per cent or higher in Math 30-1 or Pure Math 30.”
Specific Math Skills
The four skills that are mentioned repeatedly throughout the open-ended responses are student skill in the use of calculators (15 mentions), algebraic manipulation skills (15 mentions), problem-solving skills (12 mentions) and being able to connect mathematical ideas (10 mentions). Of the 15 comments regarding calculators, 3 referenced student use of calculators as a strength, for example, “The strength is using calculators for problem solving.” The rest of the comments had to do with over-reliance on calculators. One respondent stated:
A first step that doesn’t require huge changes to the whole system is to take away their calculators 90% of the time. Maybe keep them only for some experiments here and there. They are not allowed them in university, so if you want to align things, start there. At the very least, they’ll be able to do the basic operations and we can build from there. Also not having calculators suddenly causes the students stress and fear, and half the battle is fighting that fear.
Algebraic manipulation is a broad term that includes student skill in specific processes (factoring), algorithms (division algorithm) and symbolic computation. The comments regarding algebraic manipulation focused on both the weaknesses seen in students and the importance of this skill in mathematics. One participant specifically noted that he would “like students to arrive fully able to perform the division algorithm, manipulate fractions and factor polynomials. It would help if students could perform the division algorithm on polynomials.” Another stated: “Make sure students master the standard algorithms for addition and so on. Start early with algebraic symbolic computations. Other than some basic algorithms, teach more concepts and less algorithms.”
The comments regarding first-year university student problem-solving skills included analyzing a problem in order to solve it, applying learned content in new contexts, combining concepts to solve a problem and recognizing that there might be more than one way to solve a problem. One participant noted that she has “seen a significant decline in problem-solving abilities, handling of word problems.” A second participant stated:
Students are completely unwilling to experiment when faced with a problem they haven’t seen before. The suggestion to “try something and see if it works” seems like a completely foreign concept… In tutorials students will insist that they are unable to proceed with solving a problem until they are given step-by-step instructions to follow.
These two comments indicate a perceived decline in student ability to solve nonroutine problems. Other comments reflect the importance of problem solving to not only mathematics but student success in life in general: “Understanding how to formulate a problem and logically analyze it will be used by most of our students in every job they encounter.”
The most frequently identified issue (5 out of 11 comments) was lack of perseverance.
to not only mathematics but student success in life in general: “Understanding how to formulate a problem and logically analyze it will be used by most of our students in every job they encounter.”
The ability to make connections between concepts in mathematics was identified as a weakness in students both before and after 2012. Comments focused on the importance of being able to link ideas and see mathematics as a connected set of ideas as an important aspect of knowing and doing mathematics. For example, “Students struggle with the bigger picture of course material and typically memorize formulas/procedures” and “Students still see things as disjoint modules and are unable to see how they were connected.” Knowing the connections between topics and how they work together were identified as lacking in current and former students.
Student Attitudes and Behaviours
In addition to comments regarding specific content, participants identified general skills and behaviours of students that they have noticed changing over the past few years. The most frequently identified issue (5 out of 11 comments) was lack of perseverance. One participant noticed an “inability to focus on problems for long periods. They tend to give up, rather than struggle with a complex problem.” In addition, students appear to be “less willing to put in effort to learn” and “view rigorous thinking as a waste of time.” Decreased willingness to put in effort may stem from having a “lack of self-confidence in the area” or from math anxiety: “Students feel anxious about how to begin to solve a math problem.”
Other participants identified general attitudes and behaviours not necessarily specific to mathematics: “In general, it’s not about topics and skills, but they don’t have an effective approach to learning,” which points to an issue that is larger than mathematics specifically. Student expectations from faculty and instructors have also changed. One participant stated:
Present day students feel they are more “entitled” than earlier students. In a mathematics class, this becomes the expectation for the course to be a series of “type-problems” which they must learn to recognize and solve by a rote “filling in the blanks” procedure, using computations relevant to the present problem.
This is clearly antithetical to the rational thinking needed in the modern world.
This respondent sensed that students are expecting faculty or instructors to be able to categorize each type of problem that they might encounter so that the procedure to solve that problem flows from the cat-egory the problem fits within.
Three participants provided comments that focused on positive changes: “Students are very efficient and quick to arrive at an answer by closely following examples in the notes” was noted as important, but not necessarily desirable as this potentially leads students to being uncomfortable with attempting problem types that they have not seen before. One person commented that “students are more willing to work with each other on projects and are not as fearful about speaking in front of others. I think schools are doing a great job of developing the soft skill set for students.” One commented that student ability in “identifying patterns” was stronger since 2012.
Discussion
There was not a noticeable difference in knowledge, skills or behaviours in first-year university mathemat-ics students that might be attributed to the changing of the curriculum in 2012. Many of the comments from university mathematics faculty and instructors indicated that they were unsure of the difference or that there was little or no difference; some were not teaching in Alberta before 2012. Questions regarding student strengths (both before and after 2012) prompted reference to weaknesses in 13 of the 38 responses; 10 of the respondents stated that there were no strengths.
Of the 16 responses to the question regarding what should be removed from the secondary mathematics curriculum, 11 identified lack of familiarity with the content of the secondary mathematics curriculum. However, 16 recommendations for what should be included are for topics that are currently in the secondary mathematics program of studies; these included translations of absolute value functions (Mathematics 20-1 Grade 11), set theory (Mathematics 30-2 Grade 12) and solving linear equations (Mathematics 10C Grade 10). These comments could be due to student claims that they had not been introduced to those topics before, the inability of students to recall specifics about those topics or inappropriate prerequisites for university courses.
Because respondents were self-selected, the current survey may indicate stronger opinions than are present in the general instructor population. Nonetheless, the responses indicate a need for more communication between secondary and university faculty about (1) what is important in mathematics teaching and learning at both levels and (2) how high school and university courses might be better aligned in terms of what is offered in Math 30-1 and Math 30-2.
Conclusion
Based on the data collected, university preferences for Mathematics 30-1 as a prerequisite for first-year mathematics courses is appropriate for calculus and linear algebra courses, but less so for reasoning and statistics courses. Based on both the numerical and anecdotal data, there does not appear to be a common understanding among university faculty and instructors about the expectations of secondary mathematics courses. Furthermore, the curriculum change in 2012 did not seem to have a noticeable impact on student strengths in first-year mathematics courses as might have been initially thought. With this in mind, continuing conversations between university faculty and instructors, secondary teachers and curriculum developers will support clearer alignment between high school and university mathematics courses. Addition-ally, in a time of curriculum development in Alberta, including not only those university faculty and instructors who teach primarily first-year courses but also faculty and instructors from colleges and technical institutes could help make the transition from secondary to postsecondary less difficult for students in mathematics.
References
Alberta Government. 2021. Administering Diploma Exams. Alberta Government website. www.alberta.ca/administering-diploma-exams.aspx?utm_source=redirector#toc-2 (accessed January 27, 2021).
Alberta Education. 2008. Mathematics 10–12. Edmonton, Alta: Alberta Education. https://education.alberta.ca/media/564028/math10to12.pdf (accessed January 27, 2021).
Alberta Learning. 2002a. Applied Mathematics 10–20–30. Edmonton, Alta: Alberta Learning.
———. 2002b. Pure Mathematics 10–20–30. Edmonton, Alta: Alberta Learning.
Braun, V, and V Clarke. 2006. “Using Thematic Analysis in Psychology.” Qualitative Research in Psychology 3, no 2: 77–101.
Marynowski, R, and L Forand. 2016. “Pre-Requisites and Alignment of First Year Mathematics Courses and High School.” University of Calgary Department of Mathematics and Statistics Teaching Series, Calgary, Alta.
———. 2017a. “A Survey of Mathematics Professors in Alberta.” Alberta Math Dialogue, Edmonton, Alta.
———. 2017b. “University Acceptance of Alberta High School Mathematics Courses.” delta-K 54, no 1: 16–19.
———. 2017c. “A Preliminary Analysis of Mathematics Requirements in Alberta Universities.” Proceedings of the Canadian Mathematics Education Study Group Annual Meeting 2016, Kingston, Ont.
Palfy, K, P J McFeetors and L M McGarvey. 2020. “Mathematics Curriculum Change: Identifying Parental Expectations.” Journal of Research in Science, Mathematics and Technology Education 3, no 2: 51–72, DOI: 10.31756/jrsmte.322.
Richelle Marynowski is an associate professor in the Faculty of Education at the University of Lethbridge. Her teaching and research interests include class-room assessment, mathematics teaching and learning, and teacher professional development.
Landry Forand teaches at Chestermere Lake Middle School, in Chestermere. Landry started his career in 2017 as a numeracy specialist at Cochrane High School after completing his BEd and BSc in mathe-matics at the University of Lethbridge in 2016.






