Jérôme Proulx
In this article, I explore a relationship raised by Grade 5 students between equivalent halves, which can lead to a method for producing equivalent fractions “additively.” I share an account of the classroom events that led to this “adding” method and outline some mathematical explorations to understand the method.1
During the Lesson: A Relationship Between Halves
I was once in a Grade 5 classroom, working with students on fractions. At one point in the lesson, an equivalence was traced between the fractions 3/6 and 1/2. When I asked the students if they knew of other fractions equivalent to those two, some mentioned having a method for generating halves: “You take a number, double it and then place it below in the fraction.”
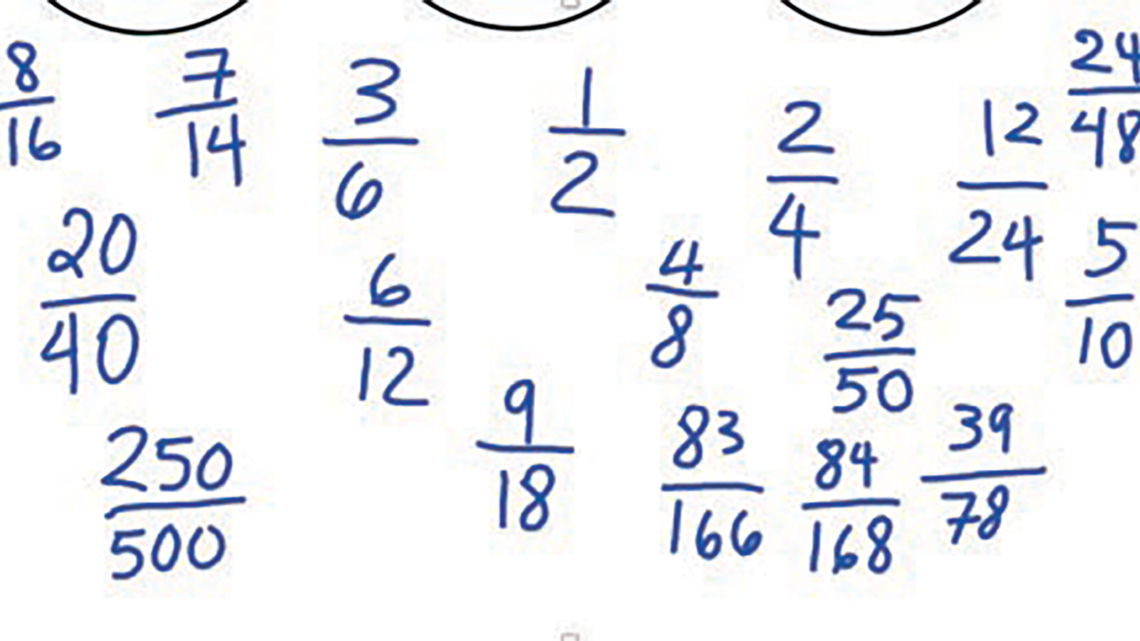
Right away, almost all their small hands were raised to offer other halves—20/40, 2/4, 6/12, 12/24, 4/8. Not anticipating the enthusiasm that would follow, I began writing these fractions on the whiteboard, close to where 3/6 and 1/2 were written, but scattered around. And it went on—25/50, 7/14, 24/48, 5/10, 250/500, 9/18, 83/166, 39/78, 84/168, 8/16. At this point, the whiteboard looked like Figure 1.
As I was about to ask them how these fractions were all equivalent and how they represented halves, a student at the front raised his hand. He had noticed something: “If you look at both 83/166 and 84/168 that Marco gave,2 they are the same. He only added 1 above and then 2 below.”
I thought that this was very interesting, although surprising. I also thought that it probably worked only with that specific pair of fractions. So, out of curiosity, I asked the students if there were other pairs of fractions that might be conceived that way. Enthusiasm once again filled the room—like “Oh, yes! There are plenty of others!”—and many hands went up.
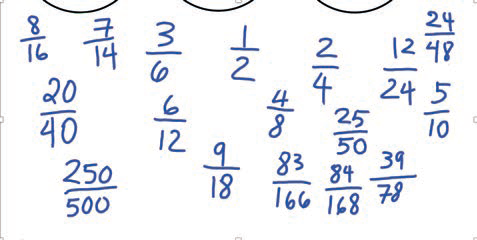
“From 1/2 to 2/4,” said one student, which I repeated slowly to make sure that it really was the same pattern of +1/+2. I was still a little puzzled by this. Another student said, “From 7/14 to 8/16.” I began to circle these pairs in green to set them apart. However, I was still thinking that only a few would follow this pattern.
Then, another student pointed out that in moving from 12/24 to 24/48, 12 and 12 were added at the numerator and 24 and 24 were added at the denominator. I circled this pair in red, since it was produced using a different “addition.”
Another student asserted, “24/48 and 25/50,” as I linked them in green. A student in the back added, “6/12 and 7/14,” and another continued, “3/6 and 4/8, as well.” Now it was becoming increasingly obvious that the pattern worked all the time and with all halves—but I could not clearly understand why.
One student returned to the doubling–adding relation-ship between 12/24 and 24/48 to link 2/4 and 4/8, with 2 and 2 added at the numerator and 4 and 4 added at the denominator. I drew a red arrow between those fractions. By then the whiteboard was a little messy. We continued, with 5/10 and 6/12, 3/6 and 6/12 (3 + 3 and 6 + 6), and 8/16 and 9/18. The board then looked like Figure 2, with green and red links all over, representing well my un-preparedness for the discovery of this kind of relation-ship between all the equivalent halves.
Somehow, in addition to the method that the students had initially mentioned (taking a number and doubling it), this +1/+2 relationship appeared to be another method for producing equivalent halves. I was well aware that this relationship would stand for ratios in proportional relationships (as I will show). However, in the context of equivalent fractions, as a relationship between or a process for producing equivalent fractions, these “additions” somehow troubled me.
First, on the spur of the moment, with my face close to the whiteboard, I could not relate this method well to the method we usually use to establish multiplicatively equivalent fractions. For example, for 1/2, we take a unit, split it in two and then take one of those two parts. Thus, 2/4 is said to be equivalent to 1/2, because for the same unit now split in four, our parts are twice as small, so we need to take twice as much to maintain the equivalence between fractions. Or if we take twice as many of these twice-as-small parts, we obtain an equivalent fraction.
Second, adding the numerators and the denominators of fractions is a minefield. A common misconception students have is that one can “add tops and bottoms together”—for example, 1/2 + 1/3 = 2/5 and 2/7 + 3/4 = 5/11 (which are incorrect).
However, now this relationship, or “adding” method, appears to fall right in the middle of these issues, lying between ratios, multiplicative equivalence and the common misconception about how to add fractions. Thus, I can say that I was as shocked by my students’ ability to find this relationship as I was by my own inability to see how it seemed to work.
Therefore, I decided to raise the question, as much for myself as for my students, of why this method worked, how it worked and whether it worked all the time. The students answered by asserting that all these halves were produced as equivalent fractions from the outset as a variety of halves, so that was simply why it worked, and that was that! Addressing my question like that led them somehow to readdress my initial question about how and why we knew that all those fractions were halves. We explored this question for the rest of the lesson, until the bell rang.
After the Lesson: Exploring This Relationship as an “Additive” Method
Although the students seemed satisfied with their explanation of halves, I still wanted to get to the bot-tom of it. I was eager to know more about it mathematically, even just for myself. For this, I needed to take a step back and make sense of all of this in terms of equivalent fractions. I offer here some of my mathematical reflections.
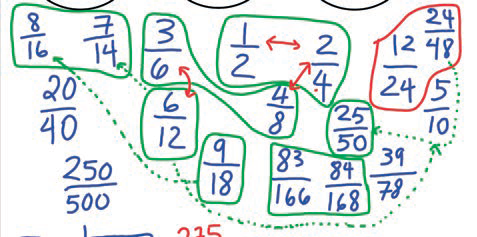
First things first. As mentioned, I am well aware that for proportional relationships, this +1/+2 relation-ship stands well. To illustrate, if I have a glass of orange juice made by diluting one part concentrated orange juice with two parts water, I have a ratio of 1:2 in terms of orange juice to water. If I add another part orange juice and another two parts water to the mix, that gives two parts orange juice for four parts water, a ratio of 2:4, which is equivalently sweet in terms of orange juice to water. Put otherwise, if I add another one part orange juice to the initial mix, I must add another two parts water to maintain the sweetness of the juice. Figure 3 represents this numerically and pictorially.
However, the various halves on the whiteboard were not about ratios; they were about equivalent fractions. And I wanted to make sense of this +1/+2 relationship precisely in the domain of equivalent fractions. I wanted to understand how this “adding” worked and why. Hence, the challenge!
To get my head around it, I attempted some algebra. I knew well that my Grade 5 students would not be familiar with this math, but this part was only for me, as a first attempt at the task.
Using the way the students explained it, we can represent halves as any fraction of the form a/2a (where the denominator is double the numerator). Then, if we add 1 to the numerator and 2 to the denominator, we get another half. This can be represented as
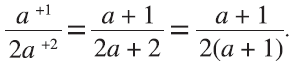
This gives another half, where (a + 1) is the number to be doubled in order to maintain the students’ structure of “take a number, double it and then place it below in the fraction.” Adding other numbers in the same “half” relationship, such as +3/+6, also works, giving us
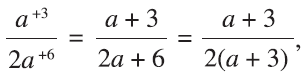
where (a + 3) is the number to be doubled in the structure of halves.
This is great and seems to produce other halves by “adding” them together, because the +1/+2 and +3/+6 act as halves as well in this “addition.” Thus, any half could be “added” to another half, adding numerators together and denominators together. With a/2a as a half and 3a/6a as another one, we get
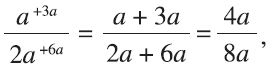
which is still in the same form. Even more generally, with a/2a as a half and b/2b as another half, we get
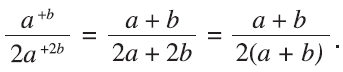
I then wondered whether this relationship, or “adding” method, would work with other kinds of frac-tions, and it did. For example, it works with or be-tween thirds:
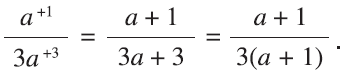
The same works for two-thirds (of the form 2a/3a):
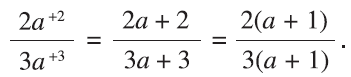
This appears quite robust. It also works for any kind of fraction in which the numbers added between them would be the numerators and the denominators. For example, with two-fifths, in the form 2a/5a “added” with 2/5, we get
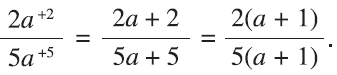
It simply works all the time!
Then, in a completely generalized form to end the algebra quest, it is possible to work with the simplified fraction in an a/b form, to which another fraction a/b is “added.” This gives us
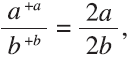
which is another equivalent fraction to a/b. If this is done with ka/kb, an equivalent fraction of a/b to which +a/+b is “added,” we get
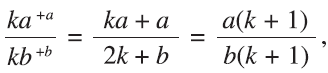
which is again an equivalent fraction to a/b and ka/kb.
Finally, with two equivalent fractions to a (namely, ka/kb and ha/hb), we get
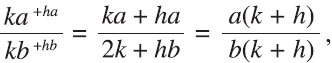
another equivalent fraction to a/b. Somehow, alge-braically speaking, this method seems to work all the time.
However, this is with algebra. Even if it seems to work, it might not be totally convincing (algebra sometimes seems magical!). Also, it is very far from the tools Grade 5 students have at their disposal. Therefore, I decided to explore the meaning of this relationship, or “adding” method, in other ways, with tools that Grade 5 students would be familiar with—words, numbers and drawings.
After the Algebra: Understanding Why This Method Produces Equivalent Fractions
Although this started as a relationship between halves, it directs one to consider it as a method for producing equivalent fractions. It does so, to some extent, by “adding” to the numerator of a fraction the numerator of an equivalent fraction, and “adding” to the denominator of a fraction the denominator of the equivalent fraction. The result is a third equivalent fraction.
Let’s look at what the method looks like numerically. With 3/6 and 1/2, we get
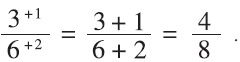
Using thirds, with 2/6 and 1/3, we get
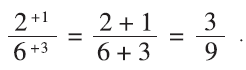
And this works with any type of fraction, as shown in the following examples.
With 1/2 = 3/6, the method gives us
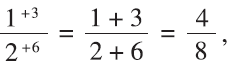
which is equivalent to 1/2.
With 1/2 = 6/12, the method gives us
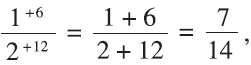
which is equivalent to 1/2.
With 4/8 = 3/6, the method gives us
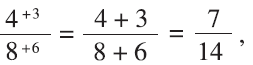
which is equivalent to 1/2.
With 1/3 = 12/36, the method gives us
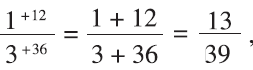
which is equivalent to 1/3.
With 2/7 = 6/21, the method gives us
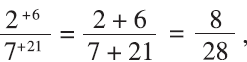
which is equivalent to 2/7.
This is really interesting! As obvious as it seems now, it is important to remember that writing out the following two equalities could appear quite puzzling at first for equivalent fractions:
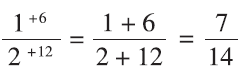
and
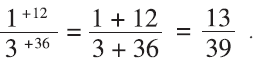
But it does work!3
That said, difficulties emerge when we attempt to verbalize what happens—to put this relationship, or “adding” method, into words. Usually, as mentioned, we explain the equivalence of fractions in multiplicative terms.
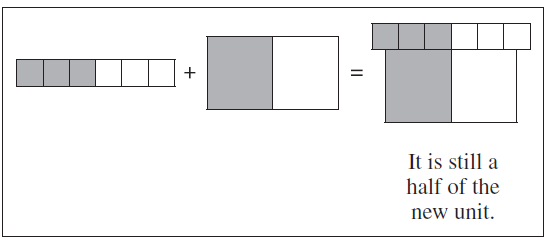
Let’s look at the example of 1/2 and 4/8. For 1/2, we take a unit, split it in two and then take one of those parts. Then, 4/8 is equivalent to 1/2 because for the same unit now split into eight (hence, four times more), our parts are four times as small. Thus, we need to take four times as many parts in order to maintain the equivalence in fractions, as depicted in Figure 4.
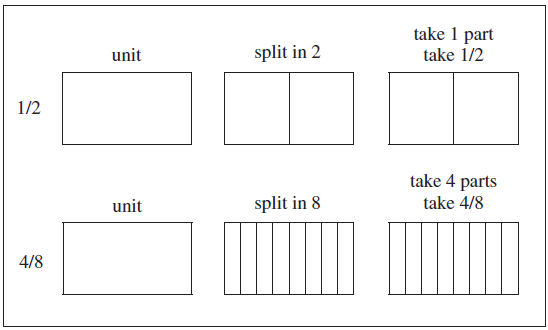
and 4/8.
However, putting into words this “adding” method to produce 4/8 from 1/2, as with
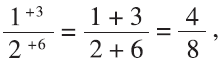
is a different and quite challenging matter. The multiplicative explanation of smaller/bigger parts and how much more/less must be taken to maintain the equivalence between 1/2 and 4/8 is hardly possible here. However, it is possible to explain it in relation to the size and the number of parts, as in the following:
I have 1/2. Thus, my unit is split into two parts, of which I take one part. I then add six more parts to the unit. I now have a new unit of eight parts. If I take an additional three parts out of all those parts of the new unit, I now have four parts out of eight, giving the equivalent fraction 4/8. Or, because I already took one part of the unit, I need to take an additional three parts out of all those parts of the new unit, which represents half of the six parts that I have just added, to maintain the equivalence. I now have taken a total of four parts out of the eight parts of the new unit—hence, 4/8.
Here, the equivalency is not talked about in multiplicative terms of how much smaller or bigger the parts become but, rather, more in terms of the number of added parts and their size. Whereas one is a multiplicative method for producing equivalent fractions, this one is “additive.”

Contrasting Units and Parts: From Equivalent Fractions to Equivalent Partitioning
The above verbalization of this relationship, or “adding” method, raises an issue concerning the unit, which is transformed in the process of adding parts to it. This transformation of the unit does not happen in the usual multiplicative explanation of equivalency, where the unit stays the same and is cut into more or fewer parts, as we saw in Figure 4.
In terms of drawing, Figure 4 also does not help much for representing the relationship, or “adding” method, as the insertion of the +3/+6 in the explanation does not explicitly appear in the drawing. In the usual multiplicative equivalency, as Figure 4 illustrates, the unit stays the same, so it is the parts that change in size. In the “adding” method, it is to some extent the opposite: the parts stay the same size, but the unit is changed. This “adding” method requires, in that sense, that we let go of the maintenance of the same unit and focus instead on the maintenance of the same size of parts, as il-lustrated in Figure 5.
The main difference lies in the fact that the parts are here kept equal, whereas the unit changes. By changing the size of the unit while maintaining the size of the parts, the partitioning is also maintained, as it is always in terms of halves. In that sense, this “adding” method can be seen to be more about equivalent partitioning than about equivalent fractions. In other words, it is about the conservation of the partitioning, not the conservation of the unit.
Going way back to the student’s example of going from 83/166 to 84/168, this is explicable numerically as follows:
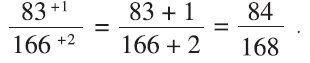
Figure 6 offers a way of illustrating this, where the +1/+2 is represented by parts of the same size as 83/166, so it maintains the partitioning but produces a new unit.
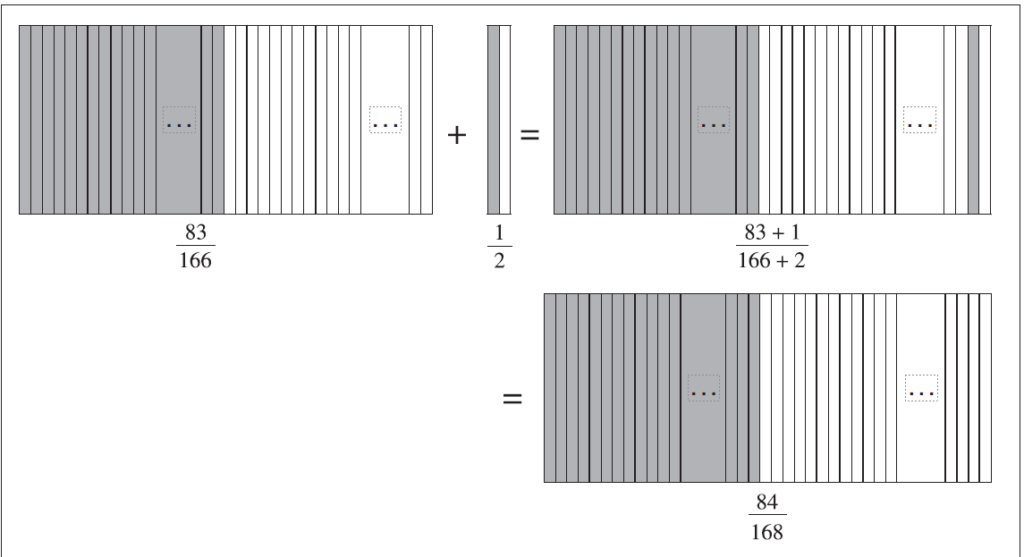
The fractions 83/166, 1/2 and 84/168 are all equivalent and all share parts of the same size, but all relate to a different unit. It is the partitioning that is maintained in each of them. The partitioning is of central importance here; it is kept for all the actions under-taken, from the first fraction, the fraction that is “added” and the resulting fraction. The partitioning of a “half” is always maintained.
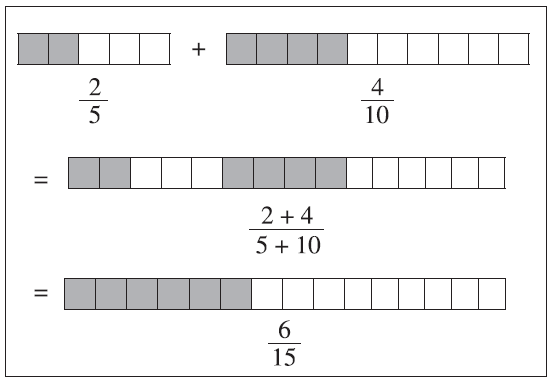
Figure 7 depicts the previously discussed equivalent fractions 2/5 and 4/10 in a similar fashion. Through this partitioning, maintaining the size of the parts makes it easier to explain (verbalize and illustrate). However, it is mostly a matter of facility of explanation, because to some extent the size of the parts of each “added” fraction does not matter. If the parts are not of the same size, then “adding” them looks a little different but works all the same. Figure 8 illustrates this for
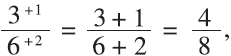
where it is clear that it is the partitioning that is central and maintained.
Concluding the Exploration
In sum, this relationship is fascinating, and this “adding” method works well. Not only does it work well, but it is also possible to explain and make sense of it using numbers, words and diagrams—all means that are available in Grade 5. Although it at first troubled me mathematically, this “adding” method has proven to be quite efficient for producing equivalences between fractions.
For sure, this way of reasoning about equivalent fractions is different from the usual multiplicative ways. As mentioned above, it is about the conservation of equal partitioning, which produces a new unit that maintains its partitioning. In this sense, this “adding” method appears to be less about equivalent fractions, which usually relates to the same unit, and more about equivalent partitioning of units. This equivalent partitioning places this relationship, or “adding” method, between fractions and ratios.
With all that said, I am not implying in any way that these ideas should be taught to Grade 5 students. I hope you’ll agree that the discovery and exploration are pleasure enough—mathematically speaking!
Notes
- Throughout the article, I put words such as additively, adding and addition in quotation marks, because what is discussed here is a different kind of addition, to say the least.
- Names have been changed to protect anonymity.
- These sequences could even be extended. For example, from
(1 +1)/(2 +2) = 2/4 to (1 +1+1)/(2 +2+2) = 3/6 to (1 +1+1+1)/(2 +2+2+2) = 4/8, and so on. This is as much surprising in terms of writing as it is in terms of a process.
Jérôme Proulx is a professor of mathematics education and runs the Laboratoire Épistémologie et Activité Mathématique (www.leam.uqam.ca) at the Université du Québec à Montréal. His research focuses on epistemological issues related to cognition and/in mathematics. His current research program is dedicated to mental mathematics and school mathematics content development. Visit his website at www.profmath.uqam.ca/~jproulx.