Mackenzie Ha, Ihn-Ah Jung and Joseline Ortiz Cardenas
While researching Eugenia Cheng, we discovered that because of her unique approach to mathematics, she is a remarkable mathematician worth knowing. Most important, the heart of her work with mathematics and beyond lies in her passion for inspiring and helping others.
Her History
Eugenia Cheng, PhD, was born and raised in Hamp-shire, UK, and her family originated from Hong Kong.1
Currently, Cheng resides in Chicago, where she teaches mathematics to art students at the School of the Art Institute of Chicago.2 At the institute, she is the scientist in residence, a position designed for a scientist who wants to contribute to the world and instill curiosity in young adults.
When Cheng is not busy teaching university stu-dents, she hosts professional development workshops for teachers around the world, does school visits and volunteers to help teach mathematics in elementary schools.3 In addition, she is an engaging public speaker who has appeared at TED Conferences in London and Vienna. She also creates online videos to educate the general public about mathematics and has authored several books.
Clearly, Cheng is passionate about teaching and uses various platforms to educate people. Her mission is “to bring mathematics to a wider audience and help reduce maths phobia.”4 To do so, she explains concepts simply and entertainingly, so that they reach a broad scope of people. She especially seeks to include those who do not have a strong background in mathematics or who have developed a fear of it. One way she helps people learn math is through making com-parisons to food, as well as revealing other unexpected connections to many aspects of our lives.
Mathematics Found in Baking
Cheng has written a number of books, and her best-known book is How to Bake Pi: An Edible Exploration of the Mathematics of Mathematics (Cheng 2015). As the publisher’s description states, the book “provides an accessible introduction to the logic and beauty of mathematics,” while also making creative parallels between mathematics and baking.5 The question she presents is, What is math and how does it work? To explore this question, she draws inspiration from the kitchen and shows that mathematics and baking share several simi-larities in their techniques and ideas. Every chapter begins with a recipe, followed by an explanation of how that recipe connects to a specific topic in mathematics.
Another example of this is a video in which Cheng (2014) uses the dessert mille feuille to explain exponents. Mille feuille is French for “one thousand layers,” and although this dessert has only three visible layers of pastry, each layer actually contains multiple layers. The process of making mille feuille shows how numbers combine together to become exponentially larger. The steps are as follows:
- Place a rectangular, flattened slab of butter on a sheet of pastry. Then fold the pastry over the butter to create two layers and roll it out until it’s flat.
- Fold the pastry into three, which creates six layers in total (2 × 3 = 6), and again roll it out until it’s flat.
- Repeat step 2 five more times (a total of six). This can be written as 2 × 3 × 3 × 3 × 3 × 3 × 3, or 2 × 36. Then, multiply by three one more time, because of the three distinct layers of pastry. The final equation becomes 2 × 37 = 4,374, signifying 4,374 layers of pastry.
Connections Between Mathematics and Social Issues
Another theme that Cheng explores is how mathematics relates to social issues, and how mathematics could be the answer to social progress. She states that “mathematics is the logical study of how logical things work” (Cheng 2018a, 8), but it does not have to be restrictive. In school, math is often taught as a set of rules to follow, but Cheng believes that mathematics should instead be something that invites students to solve problems creatively by expanding their thinking. She believes that this creative quality in math is critical. Without creativity in the world, we would not have the music and art that we enjoy. Cheng believes that progress begins with creativity and dreaming, and that mathematics is a place where that progress can be shown.
To illustrate how mathematics can help us to under-stand our world and other people and to make social progress, Cheng uses abstract mathematics. In her TED Talk (Cheng 2018b), she explains that applied mathematics involves using math in real-world situations, such as how to build a bridge or fly an airplane. She describes mathematical thinking as thinking about the human world and applying math to real issues, not just thinking about the quadratic equation.
Cheng proceeds to demonstrate how math can be used to understand the world. She begins by showing a diagram of the factors of 30. She then rearranges the diagram so that she can list the factors of 30 using only prime numbers. Then, she replaces the prime numbers with variables, so that they become abstract—able to represent anything.
Next, Cheng labels the variables according to three types of absolute privilege—rich, white and male—so that a represents a white person, b represents a rich person, and c represents a male person. She explains that this idea of absolute privilege is a sensitive subject that can make people angry. However, she believes that understanding the root of people’s anger is more productive than being angry in return.
She then looks at a diagram containing only women and adds cisgender as a variable. Although women in general feel less privileged than men, some women forget how privileged they are compared with women of different backgrounds and status. In this diagram exploring women and their comparable privilege, rich, white cis women are at the top, and non-rich, non-white trans women are at the bottom.
On the topic of gender, Cheng often shares her own experiences as a female mathematician—specifically, how she found herself having to behave a certain way to be accepted in the field. She believes that the words feminine and masculine are problematic when used to describe certain behaviours, because people have been conditioned to believe that it is wrong or undesirable for a man to be seen as feminine or a woman to be seen as masculine.
In her book x + y: A Mathematician’s Manifesto for Rethinking Gender (Cheng 2020), she encourages the use of ungendered words, such as congressive and ingressive (pp 132–33). She describes congressive as bringing things (such as people) together and ingressive as entering into things without being stopped by other people’s opinions and feelings. A person who is ingressive is focused on themself, independent, individual,
competitive and adversarial, whereas a person who is congressive is focused on the community and society, considerate toward others, interdependent, connected, collaborative, and cooperative. Cheng believes that creating a congressive environment, in which we work together instead of against each other, is better for mathematicians, schools and society.
Fascination with Higher- Dimensional Category Theory
Cheng’s main interest in mathematics is higher-dimensional category theory. Since category theory is far too complex for us to understand at this point in our education, we will reflect on what we have learned about context and content from our research and how we intend to apply these concepts in our current education, as well as in our future endeavours.
The dictionary definition of context is “the inter-related conditions in which something exists or oc-curs.”6 For example, the meaning and use of the word bark depends on the context. Is a dog barking? Or is bark referring to the bark of a tree? Content is defined as “the topics or matter treated in a written work.”7 For example, the table of contents in a book lists the chapters in that book, and those chapter titles give the reader an idea of what the book is about—or, in other words, what content the book holds.
As we were introduced to category theory, we learned that meaning should be derived from context. To take a categorical perspective in math means to consider context over content. An educational video by MathProofsable (2018) provides an analogy that helped us understand this concept. Imagine that you are in need of a spear, but all you have is a hammer. You realize that since you already have a hammer, you could sharpen its handle to make a spear. By doing this, you are deriving meaning from context by considering context over content. In one context, you could view the tool as a hammer, and in another context, you could view the same tool as a spear. This process is called recontextualizing. It is also called construction, because you are changing the context from using the tool as a hammer to using it as a spear.
We pondered how we could use these mathematical concepts in our current lives. Understanding category theory was out of our reach, but we knew that we could learn something from this simple idea of taking meaning from the context before the content. What was the point of learning about this? Figure 1, which was inspired by the MathProofsable (2018) video, illustrates some connections that showed to us the purpose of our understanding of category theory.
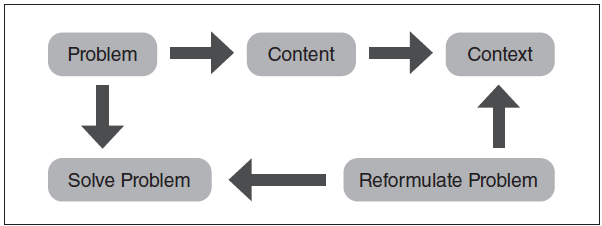
What we learned about category theory taught us the skills to solve any problem, whether in mathematics or in our lives. Guided by the steps of solving a categorical problem, the first thing we can do when we encounter a problem is to look at the content: What exactly is the problem? What does the problem contain? Once we have defined the problem and Figure 1 found the content in the problem,
we can then look at the context:
How does this problem relate to other aspects of our lives? How does x relate to y and z? Following this, we can reformulate the problem. We can rewrite or rethink the problem in a way that we can better understand or that is more relevant to any new information we have gleaned throughout the process. This will help us to eventually solve the problem by using the knowledge, structure and relationships that we found.
Because researching category theory taught us skills and strategies for solving problems through changing our perspective, we know that as we act on our new understandings, category theory will continue to show its value and help us become keen and open-minded problem solvers.
We find Eugenia Cheng incredibly inspiring be-cause of her desire to use her talents to help those who need help and those who are interested in learning more about how math works. As aspiring educators, seeing her exercise divergent thinking to work toward her goals encourages us to do the same and inspires us to use our creativity in both our future careers and our everyday lives. There are so many ways to approach learning. We just need to be innovative and discover those ways.
Notes
- Wikipedia, sv “Eugenia Cheng,” https://en.wikipedia.org/wiki/Eugenia_Cheng (accessed October 19, 2021).
- http://eugeniacheng.com (accessed December 12, 2020).
- http://eugeniacheng.com/math/about/ (accessed December 12, 2020).
- http://eugeniacheng.com/math/about/ (accessed December 12, 2020).
- www.basicbooks.com/titles/eugenia-cheng/how-to-bakepi/9780465097678/ (accessed October 19, 2021).
- Merriam-Webster, sv “context,” www.merriam-webster.com/dictionary/context (accessed December 11, 2020).
- Merriam-Webster, sv “content,” www.merriam-webster .com/dictionary/content (accessed December 11, 2020).
Mackenzie Ha, Ihn-Ah Jung and Joseline Ortiz Cardenas are undergraduate students in elementary education at Mount Royal University. With a keen interest in mathematics education, they hope to contribute to exciting educational advances through progressive and creative teaching methods. They are inspired daily by their professors, the children they teach, and each other’s positivity and diligence. They each have a variety of interests, such as playing musical instruments, creating lifestyle montage videos and learning new languages, but together they love to unwind with some bubble tea.
References
Cheng, E. 2014. “The Perfect Puff Pastry.” YouTube video, 5:32. http://eugeniacheng.com/portfolio/the-mathster-chef-perfectpuff-pastry/ (accessed October 19, 2021).
———. 2015. How to Bake Pi: An Edible Exploration of the Mathematics of Mathematics. New York: Basic Books.
———. 2018a. The Art of Logic in an Illogical World. New York: Basic Books.
———. 2018b. “How Abstract Mathematics Can Help Us Understand the World.” TEDx video, 11:17. http://eugeniacheng.com/portfolio/tedx-london/ (accessed October 19, 2021).
———. 2020. x + y: A Mathematician’s Manifesto for Rethinking Gender. New York: Basic Books.
MathProofsable. 2018. “What Is Category Theory?” YouTube video, 6:19. www.youtube.com/watch?v=jBkO1eerU8A (accessed October 19, 2021).






